(groupes ciblés : première et terminale S)
les thèmes abordés dans cette page
fonctions
numériques dérivables en un point
(1ère et terminale S)
les
asymptotes
(groupe ciblé : première S)
asymptote oblique

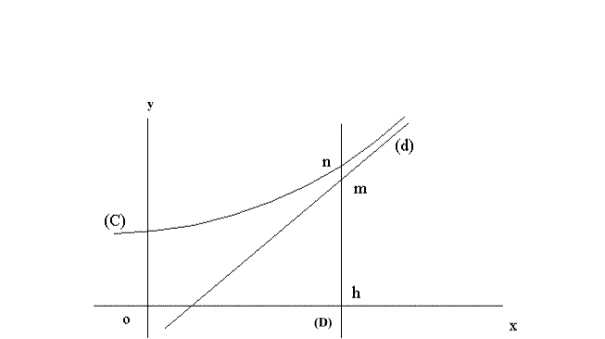
(C)
est la courbe représentative de f dans le repère orthonormal (x’ox) ;
La
droite (d) a pour équation y = ax + b
On
considère une droite (D) parallèle à l’axe y’y coupant l’axe (x’x),
(d) et (C) respectivement en h, m et n.
On
considère la quantité algébrique :
![]()
(d)
est asymptote à (C) si et seulement si la limite de cette quantité algébrique
tend vers 0 lorsque x tend
vers + ou – l’infini.
Divisons
cette quantité par x (la division est possible, puisque x tendant vers
l’infini est différent de 0) ; on obtient la
quadruple égalité (1) :
![]()
Formons
l’expression f(x) – ax ; on obtient l'égalité (2) :
![]()
Dans la quadruple égalité (1) ci-dessus, la limite du 1er membre lorsque x tend vers l’infini est 0 ; donc le dernier membre tend également vers 0 ; mais aussi la fraction :
![]()
![]()
Dans
la deuxième égalité (2) ci-dessus, la limite de
[f(x) – (ax + b)] étant 0 lorsque x tend vers l’infini, la limite de [f(x) – ax] lorsque x tend
vers l’infini est b.
Conclusion :
(d) est asymptote à (C) si et seulement si , x tendant vers + ou – l’infini, la limite « a » de l'expression :
![]()
existe et est finie.
ET
la limite « b »
de l'expression :
[f(x) – ax]
existe et est finie.
Exemple : f est définie sur R- {1} par :
![]()
![]()
et on obtient :
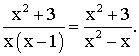
Au numérateur comme au dénominateur, on met la plus grande puissance de x en facteur ; on obtient :
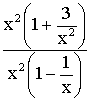
On
peut simplifier par x2 puisque
x tendant vers l’infini est différent de 0 et on obtient :
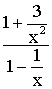
et le passage à la limite donne 1 puisque les deux fractions :
![]()
![]()
Formons
l'expression f(x) – ax ; on a :
![]()
et en mettant au même dénominateur on obtient :
![]()
Au numérateur comme au dénominateur, on met la plus grande puissance de x en facteur ; on obtient :
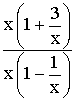
On
peut simplifier par x puisque
x tendant vers l’infini est différent de 0 et on obtient :
![]()
et le passage à la limite donne 1 puisque les deux fractions :
![]()
Ainsi
la limite de [f(x) – x] lorsque x tend vers + ou – l’infini est égale
à 1
Conclusion :
(C) admet une asymptote oblique qui est la droite d’équation y = 1.x +
1 ou
NB
:
1-
Souvent, dans des problèmes, on te demandera d’étudier la position de la
courbe (C) par rapport à son asymptote (au-dessus ou en dessous) ;
dans ce cas, c’est le signe de la quantité :
![]()
qu’il
faudra étudier ; ainsi :
si
[f(x) – (ax + b) ] est strictement positif à l’infini , (C) est au-dessus
de son asymptote,
si
[f(x) – (ax + b) ] est strictement négatif à l’infini , (C) est en
- dessous de son asymptote.
2-
(C) peut dans certains cas de problème couper son asymptote en un point x0
fini de son domaine de définition ; ceci ne change rien au fait que
(C) admet une asymptote car l’existence de cette dernière est étudiée
« à l’infini »
3-
Méthodologie pour la recherche de l’asymptote oblique
On forme d’abord l’expression :
![]()
puis on calcule sa limite lorsque x tend vers l’infini.
Si cette limite a existe et
est finie, alors on poursuit notre
recherche en formant l’expression [f(x) – ax] et en calculant sa limite b
lorsque x tend vers l’infini.
Si également cette limite b existe et
est finie, alors on conclut que (C)
admet pour asymptote oblique la droite d’équation
y = ax + b.
Si
durant cette recherche l’une au moins a et b n’existe pas ou
est égale à l’infini, alors (C) n’admet pas d’asymptote oblique.
Au
voisinage de l’infini,
la courbe (C) sera au-dessus de son asymptote oblique si et seulement
si la quantité f(x) – [ax + b] est strictement positive. Elle
sera en-dessous de son asymptote si et seulement si la
quantité f(x) – [ax + b] est strictement négative.
Asymptote
verticale
On
dira que (C) admet une asymptote verticale d’équation
x = a (a
réel fini), si et seulement si la
limite de f lorsque x tend vers a est égale à
+ ou – l’infini.
Asymptote
horizontale
On
dira que (C) admet une asymptote horizontale d’équation y = b (b réel fini), si et seulement si
la limite de f lorsque x tend vers + ou – l’infini est égale
à b.
NB :
On
a considéré dans tout ce qui précède que f était représentée
graphiquement dans un repère orthonormé ; il faut savoir que
toutes
les conclusions obtenues restent vraies dans un
repère quelconque
fonctions
numériques dérivables en un point
(groupes ciblés : première et
terminale S)
Rappel de cours
1-
Limite à gauche et limite à droite d’une fonction numérique
Soit
un réel fini fixé x0 .
On
dira que la variable réelle x tend vers x0 par valeurs inférieures
et on écrit :
![]()
lorsque x tend vers x0 en
restant strictement inférieure à x0 .
On
dira que la variable réelle x tend vers x0 par valeurs supérieures
et on écrit :
![]()
lorsque x tend vers x0 en restant strictement
supérieure à x0 .
Soit une fonction numérique f définie au point x0 .
Par définition, la limite à gauche de la fonction f lorsque x tend vers
x0 par valeurs inférieures est le réel l tel que :
![]()
La limite à droite de la fonction f lorsque x tend vers x0
par valeurs supérieures est le réel l’ tel que :
![]()
On dira que f est continue au point x0 lorsque l = l’ = f (x0).
2-
Fonction dérivable en un point et dérivée
Soit
une fonction numérique f définie au point x0 .
On dira que f est dérivable à gauche au point x0
si et seulement si :
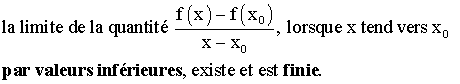
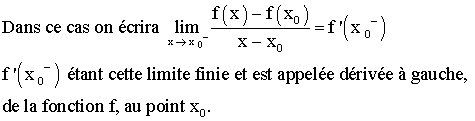
On
dira que f est dérivable à droite au point x0
si et seulement si :
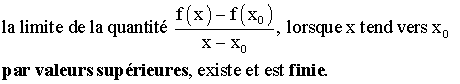
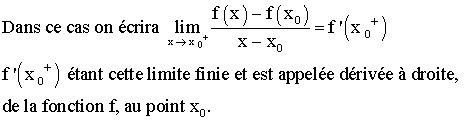
La
fonction f est dérivable au point x0
si et seulement si elle est dérivable à gauche et à
droite au point x0 et ses deux dérivées sont égales.
Ceci
signifie que l’on a :
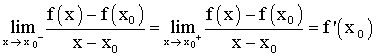
![]()
3-
Remarques
3-1

Ainsi
f est dérivable au point x0 si et seulement si :

Ainsi
utiliser l’une ou l’autre expression dans la recherche de la dérivée
revient au même.
3-2
Si
f est dérivable au point x0 , alors f est continue en ce point ;
mais la réciproque n’est pas vraie.
Ainsi
pour démontrer qu’une fonction numérique est continue en un point, il
suffit de démontrer qu’elle est dérivable en ce point ; cet énoncé
est souvent utile dans les problèmes.
Mais attention, la réciproque n’est pas vraie : une fonction peut être continue en un point sans pour autant être dérivable en ce même point.
Applications
1)
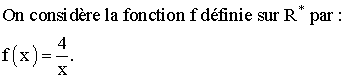
Montrer
que f est dérivable en 2 et calculer f '(2).
2)
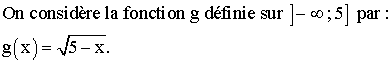
Montrer
que g est dérivable en 1 et calculer g '(1).
3)

Montrer que u
est dérivable en -3 et calculer u '(-3).
Solutions
1)
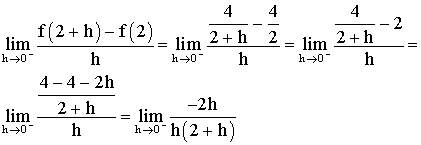
Mais h tendant vers 0 reste donc différent de 0 et on peut simplifier par h et ainsi :
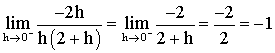
f
est donc dérivable à gauche au point 2.
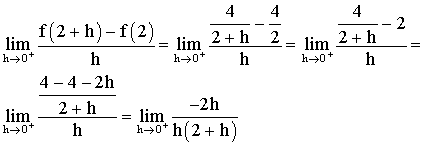
Mais h tendant vers 0 reste donc différent de 0 et on peut simplifier par h et ainsi :
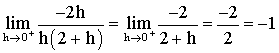
f
est donc dérivable à droite au point 2.
De
plus ces deux limites sont égales à -1.
Conclusion : f est dérivable au point 2 et sa valeur est f ’(2) = -1 .
2)
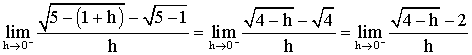
Lorsque
h tend vers 0 cette fraction prend la forme indéterminée :
![]()
Pour lever l’indétermination, multiplions le numérateur et le dénominateur par le conjugué du numérateur; il vient :
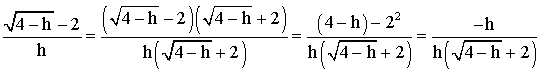
Mais
h tendant vers 0, reste différent de 0 et on peut simplifier par h :
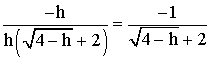
Ainsi,
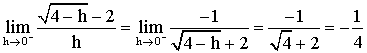
Conclusion : g est dérivable à gauche au point 1.
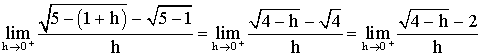
Lorsque
h tend vers 0 cette fraction prend la forme indéterminée :
![]()
Pour lever l’indétermination, multiplions le numérateur et le dénominateur par le conjugué du numérateur; il vient :
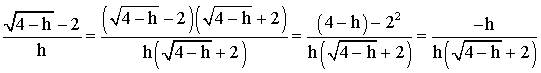
Mais
h tendant vers 0, reste différent de 0 et on peut simplifier par h :
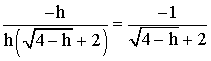
Ainsi,
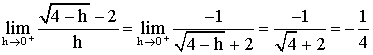
Conclusion :
g est dérivable à droite au point 1.
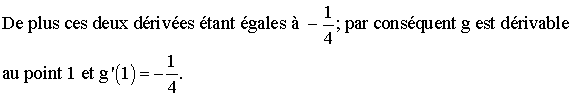
3)
Je
te laisse montrer que u est dérivable au point -3.
Tu dois trouver u’(-3)=135.
Autres applications
a-
Montre
que la fonction w définie sur R par :

Tu dois trouver les résultats suivants :
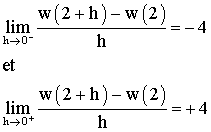
b-
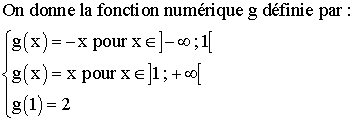
g
est-elle continue au point 1 ?
g
est-elle dérivable au point 1 ?
Trace
dans un repère orthonormal la courbe représentative Cg de g.
Tu
dois trouver comme résultats :
g
n’est ni continue, ni dérivable au point 1.
Construction de Cg :
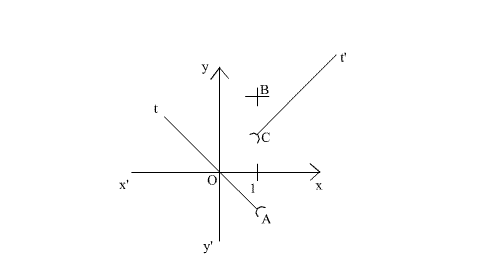
c-
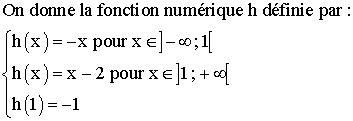
h
est-elle continue au point 1 ?
h
est-elle dérivable au point 1 ?
Trace
dans un repère orthonormé la courbe représentative Ch de h.
Tu dois trouver comme résultat :
h
est continue et non dérivable au point 1
Quant
à Ch, je te laisse la tracer.
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour le collège (page 1)
L'exercice pour le collège (page 2)
L'exercice pour le collège (page 3)
L'exercice pour le collège (page 4)
L'exercice pour le collège (page 5)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)