L'EXERCICE
POUR
LE COLLEGE
(page 2)
les thèmes abordés dans cette page
théorème
de Thalès ; maximum d’une fonction numérique
(3ème)
équations du premier degré et application
géométrique
(4ème)
propriétés des figures
géométriques remarquables; calcul d'aires
(5ème)
théorème
de Thalès ; maximum d’une fonction numérique
(groupe ciblé :
troisième)

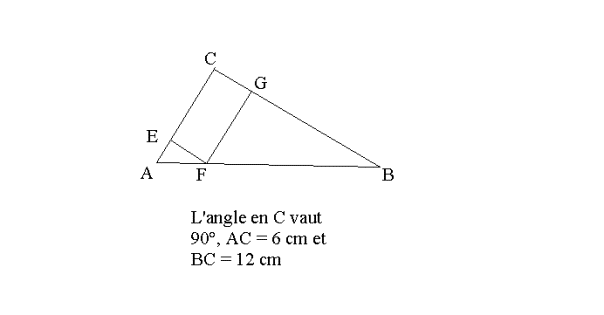
Soit ABC un triangle rectangle en C tel que
AC = 6 cm et
CB = 12 cm.
Soient E un point du segment [AC], F un
point du segment [AB],
G un point du segment [CB], tels que (EFGC) soit un rectangle.
On note AE = x
1-
Pourquoi a-t-on 0 < x < 6 ?
2-
Montrer que (EF) // (CG).
3-
En utilisant le théorème de Thalès dans le triangle (ACB),
montrer que EF = 2x
4-
En déduire l’aire du rectangle (EFGC) en fonction de x.
On notera cette aire A(x).
5-
On suppose dans cette question 5 que EA = 2 cm.
Calculer alors l’aire de (EFGC).
6-
On suppose dans cette question 6 que EA = 0,2 cm.
Calculer alors l’aire de (EFGC).
7-
Quelle doit être la position du point E pour que l'aire du rectangle (EFGC) soit maximale ?
Solution
1-
E se déplace tout en restant élément du segment [AC]. Il décrit ce segment en allant de A (x = 0) à C (x = 6) ; donc :
![]()
Si on écarte
le cas où le rectangle se réduit à un segment (E en A) et le cas où il se réduit
à un point (E en C), alors 0 <
x < 6
2-
On sait
que dans un rectangle les côtés opposés sont parallèles.
Or le
quadrilatère (EFGC) étant un rectangle, ses côtés opposés sont parallèles
et ont des mesures égales.
Donc (EF) // (GC) ou (EF) // (BC)
3-
On sait
que dans un triangle, une droite parallèle à un des côtés et rencontrant les
deux autres côtés, partage ces derniers en des segments dont les mesures sont
respectivement proportionnelles (théorème
de Thalès)
Or dans le triangle (ABC), on a (EF) // (BC) ; donc :
![]()
On sait que BC = 12 cm, AC = 6 cm et AE = x

4-
On sait
que l’aire du rectangle (EFGC) est EF.EC = (2x).EC
Or EC = AC – AE = 6 – x
Donc A(x) = 2x(6 - x)
5-
A(2) = ?
Il suffit
de remplacer dans A(x) = 2x(6 - x), x par 2 et on obtient :
A(2) = 4(6 - 2) cm2 = 16 cm2
6-
A(0,2) = ?
Il suffit
de remplacer dans A(x) = 2x(6 - x), x par 0,2 et on obtient :
A(0,2) =
2.(0,2)(6 – 0,2) = 0,4(5,8) cm2 = 2,32 cm2
7-
On sait que deux nombres variant tels que leur somme reste constante, leur produit atteint son maximum lorsqu’ils deviennent égaux.
Or :
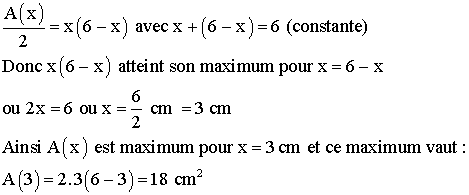
Conclusion: l'aire de ce rectangle est maximum lorsque le point E se confond
avec le milieu du côté [AC].
équations du premier degré et application
géométrique
(groupe ciblé : quatrième)
Partie 1
On te donne la figure suivante : (ABCD) est un carré dont la mesure commune de ses côtés est x cm.
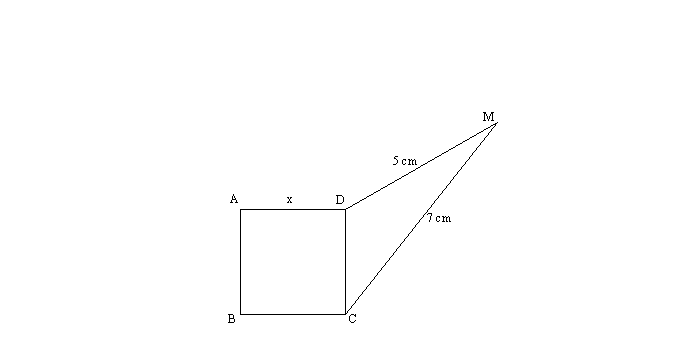
(CDM) est un triangle dont les côtés [DM] et [CM] ont respectivement pour mesures 5 cm et 7 cm.
Calculer l'aire du carré sachant que son périmètre est égal à celui du triangle.
Partie 2
Ta maman a envoyé ton frère aîné acheter du
jus d'ananas à l'épicerie d'à côté.
Il prend un paquet de six bouteilles et se présente à la caisse.
La caissière lui précise alors qu'il lui manque 0,19 €.
Il revient au rayon et pose une bouteille, puis
se présente de nouveau à la caisse et paye.
La caissière lui rend alors 0,95 €.
Quel est le prix d'une bouteille de jus ?
Combien d'argent avait ton frère avant l'achat ?
Solution
Partie 1
Pour
pouvoir calculer l’aire du carré, il faudra calculer d’abord la mesure
commune des ses côtés qui est x.
Dans
ce cas, le périmètre du carré est 4x
Celui du triangle est x + 5 +7 = x + 12
On
sait que ces deux périmètres sont égaux ; donc :
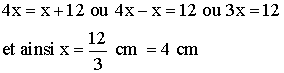
L’aire
du carré est donc x2 = 42 cm2 ou encore 16 cm2
Partie 2
Posons
y le prix en euros d’une bouteille.
Au premier passage de mon frère à la caisse, la caissière lui indique qu’il
lui manque 0,19 €.
Donc
la somme d’argent qu’il avait est 6y – 0,19
Au
second passage, il n’avait plus que 5 bouteille et la caissière lui rend
0,95 € ; donc la somme d’argent qu’il avait est également
5y
+ 0,95
En égalisant ces deux expressions et en résolvant l’équation dont l’inconnue est y, on obtient :
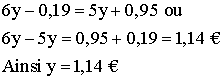
Mon frère avait donc avant l'achat :
(5 x 1,14) + 0,95 € ou 6,65 €
propriétés des figures
géométriques remarquables; calcul d'aires
(groupe ciblé :
cinquième)
Partie 1
(ABC) est un triangle
rectangle et isocèle dont l'angle au sommet B est droit.
M est un point du plan contenant (ABC) tel que (AM) est parallèle à (BC) et
(MC) est parallèle à (AB).
Montre que le quadrilatère (ABCM) est un carré.
Partie 2
On donne un cercle quelconque
(C) de centre O.
[MQ] et [NP] sont deux diamètres non perpendiculaires de ce cercle.
Montre que le quadrilatère (PMNQ) est un rectangle.
Partie 3
Calcule les aires des surfaces coloriées suivantes :
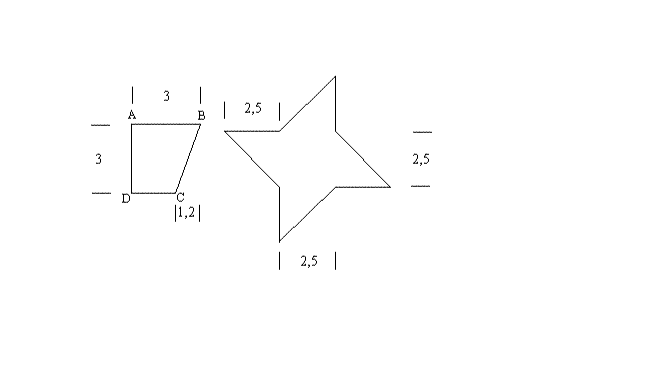
NB : les mesures sont données en centimètre. Les branches de
l'étoile sont des triangles rectangles isocèles.
Solution
Partie 1
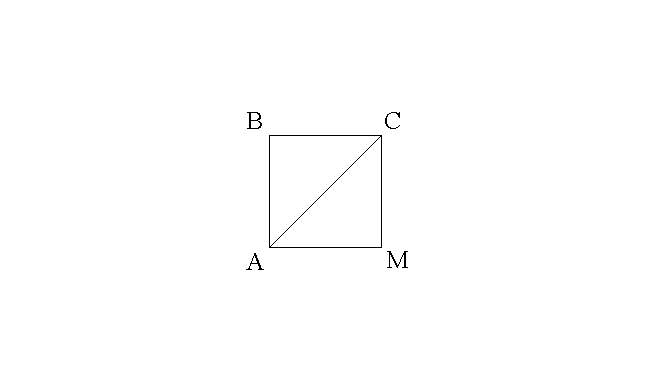
On sait que tout
quadrilatère ayant ses côtés deux à deux opposés et parallèles est un
parallélogramme.
Comme (AM) est parallèle à (BC) et
(MC) est parallèle à (AB), alors (ABCM) est un parallélogramme.
On sait que tout
parallélogramme ayant un de ses angles intérieurs droit est un
rectangle.
Comme l'angle intérieur au sommet B du parallélogramme (ABCM) a pour mesure
90°, alors (ABCM) est un rectangle.
On sait que tout rectangle
ayant deux côtés adjacents de mesures géométriques égales est un carré.
Comme (ABC) est un triangle rectangle isocèle, donc AB = BC, alors le rectangle
(ABCM) possède deux côtés adjacents [AB] et [BC] tels que AB = BC et ainsi
(ABCM) est un carré.
Partie 2
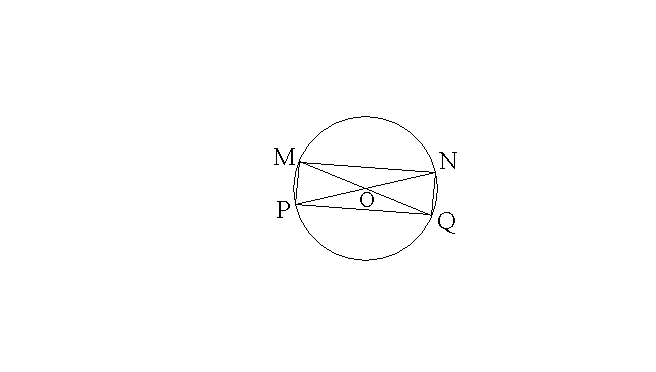
On sait que tout quadrilatère ayant les diagonales se coupant en leur milieu et de mesures géométriques égales est un rectangle.
Comme [MQ] et [NP] sont deux
diamètres d'un même cercle, alors ils se coupent en leur milieu qui est le
centre O et ont la même mesure géométrique.
Alors le quadrilatère (PMNQ) est un rectangle.
Partie 3
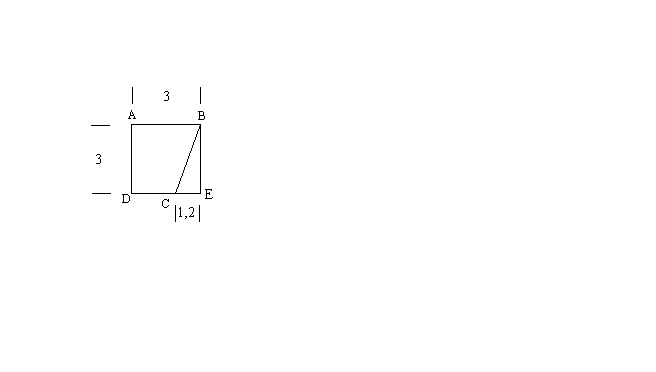
Complétons la figure en prolongeant les droites (DC) et et la perpendiculaire menée de B à (AB); ces deux droites se coupent en E.
Si A est l'aire du triangle rectangle (BCE), alors :
![]()
Si B est l'aire du carré (ABED), alors :
![]()
L'aire du trapèze (ABCD) sera donc :
![]()
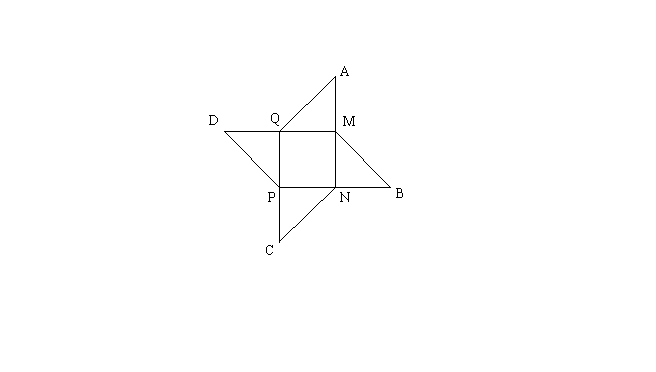
Les
quatre branches de l'étoile sont toutes identique à un triangle rectangle
isocèle. Donc l'aire totale de ces quatre branches sera
égale à l'aire de
l'une d'elle multipliée par 4.
Appelons S cette aire, alors :
![]()
Si S' est l'aire du carré (MNPQ), alors :
![]()
L'aire de l'étoile sera donc :
![]()