
L'EXERCICE
POUR
LE COLLEGE
(page 3)
les thèmes abordés dans cette page
divisibilité; temps et partage
(6ème)
fractions; échelle et repérage
(5ème)
construction
géométrique et isométrie
(3ème)
distance, vitesse et temps
(4ème)
divisibilité; temps et partage
(groupe ciblé : sixième)
Partie 1
a-
Donne les nombres entiers naturels divisibles par 5 et compris entre 231 et 262.
b-
Donne les nombres entiers naturels divisibles à la fois par 5 et par 9, compris entre 1207 et 1409.
Partie 2
Raoul, gagnant dans une course, est parti à 14 h
12 min 27 s et est arrivé à 16 h 28 min 19 s.
En combien de temps a-t-il parcouru le trajet de la course ?
Partie3
Raymond, Aurélien et Corinne achètent ensemble
une boîte de 12 cassettes audio pour un montant de 33 €.
Raymond en prend 5, Aurélien 3 et Corinne le reste.
Combien vont-il payer chacun ?
Solution
Partie 1
On sait qu'un entier naturel est divisible par 5
si son chiffre d'unités est 0 ou 5.
Ainsi les entiers compris entre 231 et 262 sont :
235; 240; 245; 250; 255; 260.
Partie 2
Il faudra effectuer la soustraction suivante :
16 h 28 min 19 s - 14 h 12 min 27s
Cependant on ne peut pas l'effectuer directement car 27 s > 19 s; il faudra donc préalablement, prendre 1 min des 28 min, la convertir en secondes et ajouter le résultat à 19 s.
Ainsi la soustraction devient :
16 h 27 min 79 s - 14 h 12 min 27 s et le résultat est 2 h 15 min 52 s.
Partie 3
Construisons le tableau de proportionnalité.
On
a, en posant A, B et C les prix que payent
respectivement Raymond, Aurélien et Corinne :

D'après ce tableau on obtient par la règle de proportionnalité :

fractions; échelle et repérage
(groupe ciblé : cinquième)
Partie 1
calculer a, b, c et d sachant que :

Solution
Avant de procéder au calcul il faudra simplifier s’il y a lieu.


Partie 2
1)
La longueur d'une parcelle de terrain est 12,80 mètres. Sur un plan, elle est
représentée par une longueur de 32 cm.
Quelle est l'échelle de ce plan ?
Solution
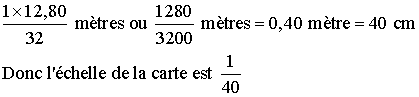
2)

Solution
1 cm sur la carte représente 5000000 cm = 50 km sur le terrain ; les 20,40 cm sur la carte représenteront donc :
![]()
3)

Solution
2000000 cm = 20 km sur le terrain représentent 1 cm sur la carte ; donc 760 km sur le terrain représenteront sur la carte :
![]()
4)
La largeur horizontale d'une emprise d'une rue est de 6 mètres de chaussée et
de 1,80 mètres de largeur de trottoir, de part et d'autre de la chaussée.
Quelle est la largeur réduite sur le plan de l'ingénieur responsable d'un
projet d'élargissement de la rue, sachant que l'échelle de ce plan est 1/500 ?
Le trottoir sera élargi de 0,50 mètre; quel est l'élargissement qui sera
indiqué par AutoCad*.
NB : AutoCad est un logiciel permettant à l'ingénieur de saisir graphiquement un projet de construction d'une rue ou d'une route et de préparer son dossier en vue de la réalisation de ce projet.
Solution
On
a une chaussée de 6 m de large et deux trottoirs de 1,80 m de large, chacun ;
donc l’emprise totale est 6 + 2 x 1,80 m = 9,60m.
500 cm = 5 m sur le terrain représentent 1 cm sur le plan ; 9,60 m représenteront
donc sur le plan :
![]()
Le
trottoir sera élargi de 0,5 m ; donc en tout 2 x 0,5 m = 1m (car on a deux
trottoirs).
5 m sur le terrain représentent 1 cm sur le plan ; donc 1 m sur le terrain
représentera sur le plan :
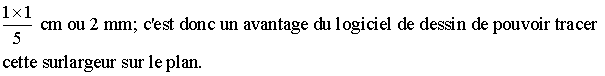
Partie 3
Sur un axe (x'x) gradué en centimètre, orienté et d'origine O, on place les points A, B, C et D d'abscisses respectives +1, -3, -2 et +4.
1)
calcule les distances AC et BD.
2)
Sachant que M et N sont respectivement les milieux des segments [AC] et [BD],
calcule les abscisses xM et xN de M et N.
Calcule la distance MN.
Solution
Rappel de cours :

1)
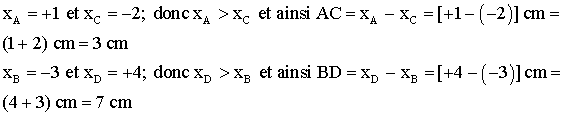
2)
M étant milieu de [AC], on a :
![]()
N étant milieu de [BD], on a :
![]()
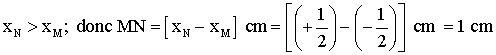
construction
géométrique et isométrie
(groupe
ciblé : troisième)
On considère un triangle (ABC) isocèle en A dans lequel la médiatrice
du côté [AC] coupe la droite (BC) en un point D extérieur à [BC].
Soit E le point de la demi-droite [DA)
tel que E n’appartient pas au segment [DA] et AE=BD.
1- Quelle est la condition que doit
satisfaire le triangle (ABC) pour que la figure soit possible ;
construis-la.
2- Montre que les triangles (ABD) et (CAE)
sont isométriques.
3- Quelle est la nature du triangle (DCE).
Solution
1-
Construction
de la figure.
Si la mesure a de l’angle au sommet A vaut 60°,
alors le triangle isocèle (ABC) devient équilatéral et
la médiatrice (d) de [AC] est à la fois hauteur et
bissectrice ; et dans ce cas , (d) passe par B et ainsi B et D sont
confondus.
Ceci ne correspond pas à l’hypothèse de l’énoncé qui dit que le point D
doit être à l’extérieur du côté [BC].
![]()
Étudions le cas où a < 60°
Montrons alors que le point D ne peut appartenir à [BC].
Supposons le contraire, c’est-à-dire que D appartient à [BC] ; et soit la figure correspondante ci-dessous :
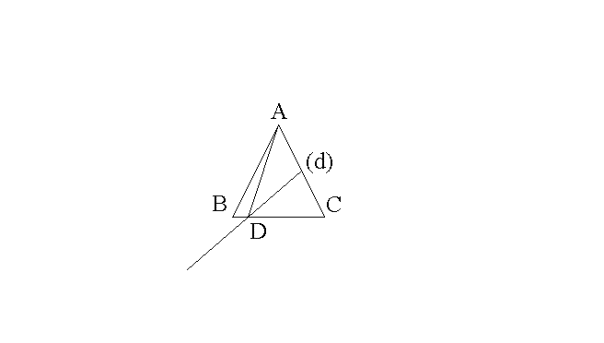
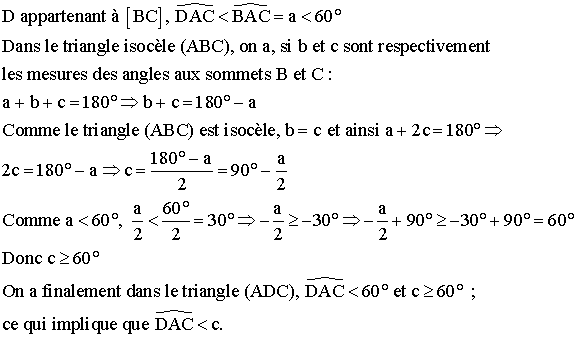
On sait que dans un triangle, des deux côtés quelconques, celui qui a la mesure géométrique la plus grande est le côté opposé à l’angle dont la mesure est la plus grande.

Conclusion : D n’appartient pas à [BC], c’est-à-dire que D est à l’extérieur du segment [BC].
Le cas où a > 60° implique que D appartient au segment [BC].
Pour construire la figure selon les hypothèses de l’énoncé, c’est-à-dire le point D à l’extérieur du côté [BC], il suffit donc de prendre un angle au sommet A de mesure a telle que 0° < a < 60°.
La figure correspondante à ce cas est la suivante :

2- Démonstration
que les triangles (ABD) et (AEC) sont isométriques.


les triangles (ABD) et (EAC) sont isométriques
car ils ont un angle isométrique compris entre deux côtés
respectivement isométriques.
3- Nature du triangle
(DCE)
Les triangles (ABD) et (EAC) étant isométriques,
les angles en D
et E respectivement opposés aux côtés isométriques [AB] et [AC], sont
isométriques et par conséquent le triangle (DCE) est isocèle
car il a deux de ses angles isométriques.
distance, vitesse et temps
(groupe ciblé : quatrième)
Deux villes A et B sont sur un axe
droit, distantes de 850 km.
Un voiture M part de A vers B à la vitesse constante de 80 km/h et une autre
voiture N part au même instant de B vers A à la vitesse de 90 km/h. le départ
simultanée a lieu à 8h.
On te demande de calculer l'instant auquel ces deux voitures vont se croiser et
à quelle distance de A ce croisement aura lieu.
Solution
Orientons la droite (AB) avec le
sens positif de A vers B. Considérons A l'origine de cet axe.
Posons x la distance qui sépare la ville A du point de croisement de ces deux
véhicules et t l'instant auquel ce croisement a lieu.
L'équation horaire du véhicule M
est donc :

L'équation horaire du véhicule N
est :


Les deux véhicules M et N se croiseront à 13 heures.

M et N se croiseront donc à 400 km de la ville A.