L'EXERCICE
POUR
LE COLLEGE
(page 5)
les thèmes abordés dans cette page
équation
d'une droite et calculs trigonométriques
(3ème)
fonction numérique et résolution d’équations
(3ème)
développement
et factorisation
(3ème)
équation
d'une droite et calculs trigonométriques
(groupe
ciblé : troisième)
Partie 1
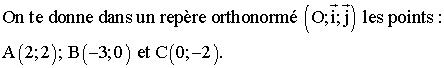
L’unité de longueur prise sur les axes est le
centimètre.
1-
Trouve l’équation de la hauteur du triangle (ABC) abaissée de
A.
Soit H le pieds de cette hauteur.
Trouve les cordonnées de H et calcule AH.
2-
Calcule l’aire du triangle (ABC)
3-
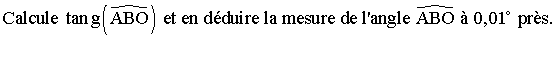
4-
![]()
5-
En t’inspirant des questions 3 et 4, calcule les mesures de l’angle au
sommet C du triangle (ABC) et en déduire celle de l’angle au sommet A.
Solution
1-
L’équation de la hauteur du triangle (ABC) abaissée de A est de la forme :
y = ax + b
Elle passe par le point A ; donc les coordonnées de A doivent la vérifier et on a donc :
yA = axA + b ou encore 2 = 2a + b
Trouvons l’équation de (BC).
Elle est de la forme y = mx + n et passe par B et C ; donc les coordonnées
de B et de C devront vérifier cette équation et on a donc :
yB = mxB + n et yC = mxC + n ou
encore 0 = -3m + n et –2 = 0m + n
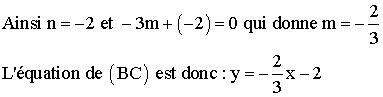
Par ailleurs la hauteur abaissée de A devant être
perpendiculaire à (BC), le produit des coefficients directeurs des équations
de ces deux droites devra être égal à –1 ; donc on a :
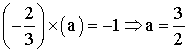

H appartient à la fois à (BC) et à cette
hauteur ; ses coordonnées devront vérifier simultanément les deux équations
et on a :
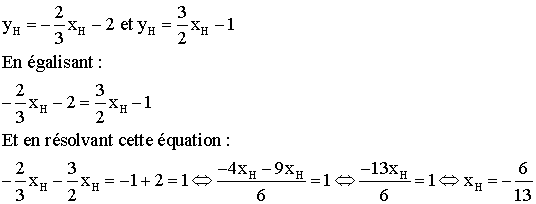
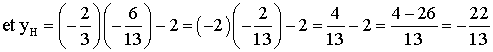
Le théorème de Pythagore donne :
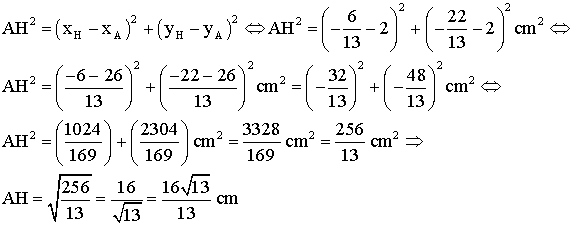
2-
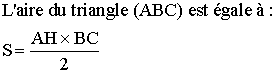
On a calculé AH ; il nous reste à calculer BC.
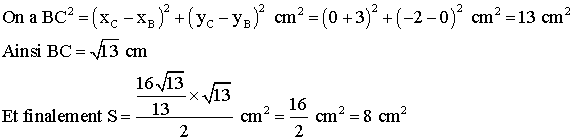
3-
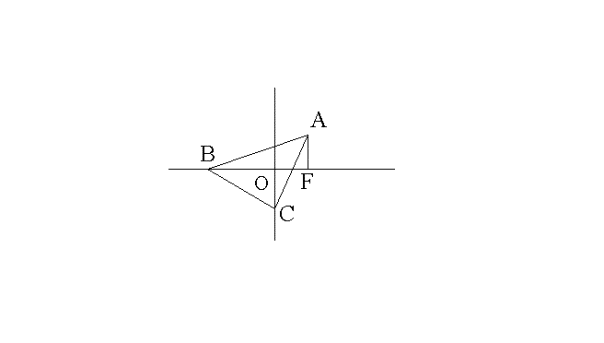
Soit F la projection orthogonale de A sur l’axe des abscisses.
Dans le triangle (ABF) rectangle en F, on a :
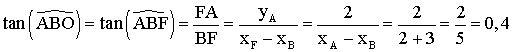
![]()
4-
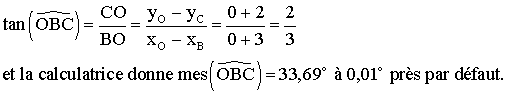
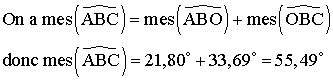
5-
Soit K la projection orthogonale de A sur l’axe des ordonnées.
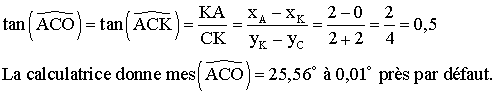
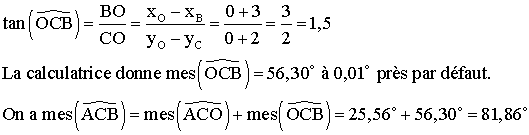
On sait que dans un triangle, la somme des
mesures des trois angles intérieurs est égale à 180° .
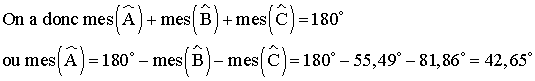
Partie 2
On donne la mesure a d’un angle aigu dont le
sinus vaut 0,355.
Calcule cos(a) et tan(a).
solution
Rappel de cours


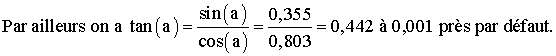
fonction numérique et résolution d’équations
(groupe
ciblé : troisième)
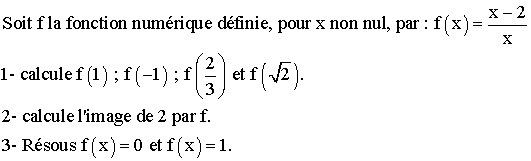
solution
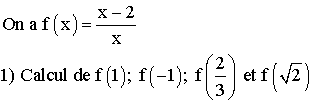
Pour calculer f (x0 ) il suffit de
remplacer dans l’expression de f (x), x par x0 .
Ainsi on a :
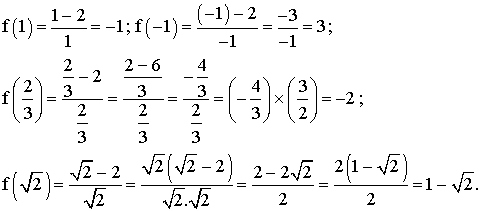
2) Calcul de f (2)
![]()
3) Résolution des équations f (x) = 0 et f (x) =1
Notons d'abord que ces équations n'ont de sens
que pour x appartenant au domaine de définition de la fonction f,
c'est-à-dire
pour les valeurs du dénominateur x différentes de 0.

développement
et factorisation
(groupe
ciblé : troisième)
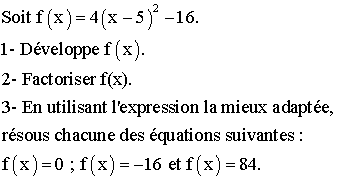
solution
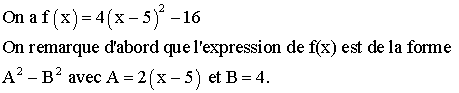
1) Développement de f(x)
![]()
2) Factorisation de l’expression de f(x)
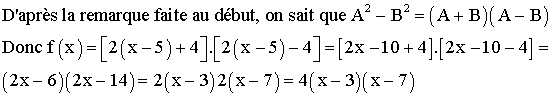
3) Résolution d’équations
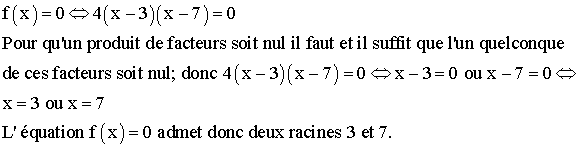
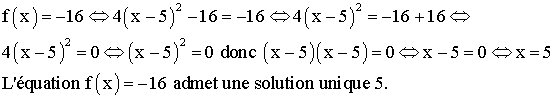
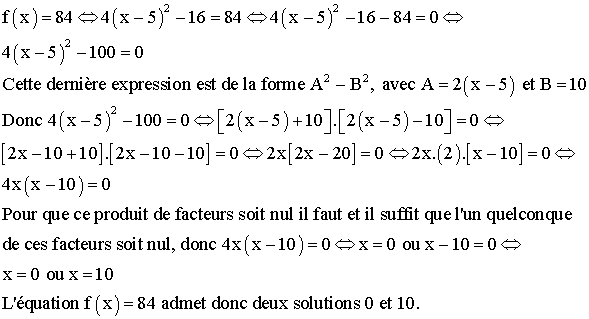
Les autres pages
Un mot sur le fonctionnement de Lam aleph
Exerce - toi (page 2)
L'atelier du
collégien (1)
Il était une fois...le passé dans le présent
Quoi encore ?...Quoi de neuf ?...(1)
Quoi encore ?...Quoi de neuf ?...(2)
Non nova , sed nove...(page 1)
Non nova , sed nove...(page 2)
L'exercice pour la seconde et la première S (page 1)
L'exercice pour la seconde et la première S (page 2)
L'exercice pour la seconde et la première S (page 3)
L'exercice pour la seconde et la première S (page 4)
L'exercice pour la seconde et la première S (page 5)
L'exercice pour la seconde et la première S (page 6)
L'exercice pour la terminale L (page 1)
L'exercice pour la terminale L (page 2)
L'exercice pour la terminale L (page 3)
L'exercice pour la
terminale L (page 4)
L'exercice pour
la terminale S (page 1)
L'exercice pour la terminale S (page 2)
L'exercice pour la terminale S (page 3)
L'exercice pour la terminale S (page 4)
L'exercice pour la terminale S (page 5)
L'exercice pour la terminale S (page 6)
L'exercice pour la terminale S (page 7)