L'EXERCICE
POUR LA SECONDE ET LA PREMIERE S
(page 2)
les thèmes abordés dans cette page
barycentre d’un système ;
variation d’une fonction numérique composée
(1ère S)
droites et plans orthogonaux
(2de)
barycentre d’un système ;
variation d’une fonction numérique composée
(groupe ciblé : première S)
(ABC) est un triangle du plan
(P).
A' B' et C' sont milieux respectifs des segments [BC], [CA] et [AB].
Le point D est défini par l'égalité vectorielle :
![]()
On donne la fonction numérique f définie sur l’intervalle [-2 ;2] par :
![]()
On demande d’écrire l’expression de f sous la
forme :
![]()
Etudier la variation de f.
Pour le système {A(2) ;
B(1) ; C(1)}, D est barycentre de
{A(2) ; B(1)},
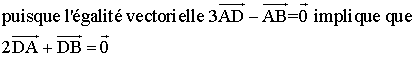
et G est barycentre de {
D(3) ; C(1)} et ainsi G appartient à (CD).
On a donc :
![]()
Mais aussi,
![]()
![]()
Donc dans le triangle (DBC),
(C’G) est parallèle à (BC) ; ce qui implique que G appartient à (C’B’).
Par ailleurs G est barycentre de {A(2) ; B(1) ; C(1)}, puisque D est
barycentre de { A(2) ; B(1)} et G est barycentre de { D(3) ; C(1)}.
Comme A’ est barycentre de {
B(1) ; C(1)}, G est barycentre de
{ A’(2) ; A(2)} et ainsi on
a :
![]()
D’où G appartient
également à (AA’).
Conclusion :
G appartient à (CD) ; G
appartient à (C’B’) et G appartient à (AA’) ; donc (CD), (C’B’)
et (AA’) sont concourantes et leur point d’intersection est le barycentre G
du système {A(2) ; B(1) ; C(1)}.
Considérons
les fonctions numériques suivantes :

Comme
la fonction u n’est pas monotone sur [-2 ;2], on doit étudier la
monotonie de f sur [-2 ;0] puis sur ]0 ;2].
![]()
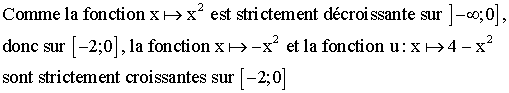
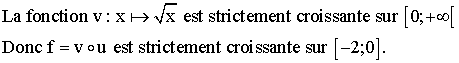
![]()
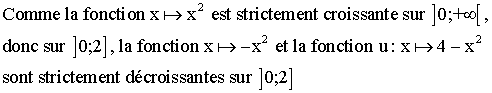
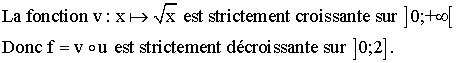
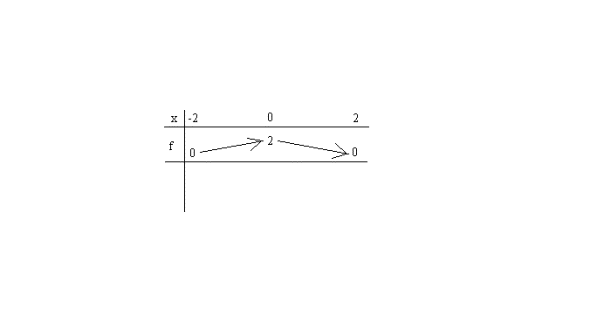
D’où
le tableau de variation de f :
droites et plans orthogonaux
(groupe ciblé :
seconde)
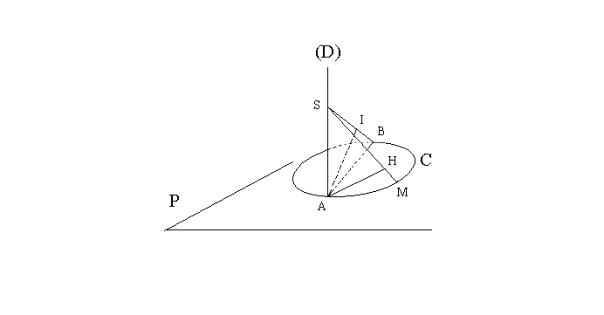
Dans un plan (P), on considère un cercle C de diamètre [AB]. Soit (D) la droite passant par A orthogonale à (P) et S un point de (D) distinct de A.
On
note I le projeté orthogonal de A sur la droite (BS). Pour tout point M du
cercle C, distinct de A et de B, on note H le projeté orthogonal de A sur la
droite (MS).
1)
Montrer
que la droite (MB) est orthogonale au plan (AMS).
2) En déduire que la droite (AH) est orthogonale au plan (BMS).
1)
M appartient au cercle C, [AB] est un diamètre
de C, le secteur angulaire de sommet M et de côtés [MA) et [MB) est inscrit
dans C et intercepte [AB] ; donc ce secteur est droit et ainsi (MB) est
perpendiculaire à (MA).
(AS) est incluse dans (D). (D) étant orthogonale à (P), est orthogonale à toute droite incluse dans (P) et en particulier (D) est orthogonale à (MB).
Ainsi (AS) est orthogonale à (MB).
On sait qu’une droite est orthogonale à un plan si et seulement si elle est orthogonale à deux droites concourantes de ce plan.
Comme (MB) est orthogonale à (MA) et (AS), deux droites concourantes du plan (AMS), alors (MB) est orthogonale au plan (AMS).
2)
(MB) étant orthogonale au plan (AMS), est orthogonale à toute droite incluse dans ce plan et en particulier à (AH).
Mais H étant le projeté orthogonal de A sur la droite (MS), on a (AH) orthogonale à (SM).
Ainsi, la droite (AH) étant orthogonale aux deux droites concourantes (MB) et (MS) du plan (BMS), est orthogonale à ce plan.
page 1 page 3 page 4 page 5 page 6