2ème partie
D'abord tu dois calculer l'augmentation subie par l'objet, c'est-à-dire :
En conclusion, cet objet coûte aujourd'hui (260 + 780) € = 1040 €.
L'EXERCICE
POUR
LE COLLEGE
(page 1)
les
thèmes abordés dans cette
page
les pourcentages
(6ème)
la
logique, les vitesses et le calcul du volume d'un solide
(5ème)
Thalès, Pythagore et trigonométrie
(4ème)
applications linéaire et affine; système d'équations
(3ème)
un peu d'arithmétique quotidienne
(groupe ciblé : sixième)
1ère partie
J'ai été livré d'une machine
électroménagère dont le prix TTC est de 1200 €.
J'ai déjà versé 30 % à la commande.
Combien me reste- t-il à payer au fournisseur ?
2ème partie
Dans un pays, les prix ont augmenté de 300 % en
un seule année. Combien coûte aujourd'hui un objet qui valait 260 € il
y a un an ?
Ta montre valait l'année dernière 50 €. Combien aujourd'hui tu l'aurais
payée dans ce pays ?
3ème partie
J'ai acheté 4 revues ayant le même prix et un
quotidien qui vaut 1,50 €.
Je donne au libraire 20 € et il me rend 6,50 €.
Combien coûte une revue ?
Solutions
1ère partie
Je dois d'abord calculé les 30 % des 1200 €.
(1200 x 30) : 100 € = 360 €.
Il me reste donc à payer :
1200 € - 360 € = 840 €.
2ème partie
D'abord tu dois calculer l'augmentation subie par l'objet, c'est-à-dire :
![]()
En conclusion, cet objet coûte aujourd'hui (260 + 780) € = 1040 €.
L'augmentation subie par ma
montre est de
![]()
Donc je l'aurais payée aujourd'hui, dans ce pays,
(50 + 150) € = 200 €.
3ème partie
D'abord je dois calculé le coût
total de mes achats :
(20 - 6,50) € = 13,50 €.
Ensuite, j'en déduis le coût du quotidien pour trouver celui des 4 revues :
13, 50 € - 1,50 € = 12 €.
En conclusion, le prix d'une revue est de :
![]()
logique, calcul numérique et géométrie
(groupe ciblé : cinquième)
1ère partie
Un bassin est vide et est muni de deux robinets
dont l'un l'alimente en eau à la vitesse de 0,5 litre par seconde et l'autre le
vidange à la vitesse 39 litres par minute.
A 8h j'ouvre simultanément les deux robinets.
A quelle heure sera-t-il plein ?
2ème partie
Un vase cylindrique possède 0,8 dm de rayon et 30 cm de hauteur.
Calcule son volume en dm3 , puis en litres (1 litre = 1 dm3 ) .
Sachant qu'un verre d'eau contient 0,18 litre d'eau, combien dois-tu verser de verres pour remplir la vase ?
On prendra
![]()
3ème partie
Un barrière pleine en béton a la forme d'un parallélépipède rectangle dont la base a pour dimensions 10 cm et 20 cm. La hauteur de cette barrière est de 25 cm.
On pose sur sa partie supérieure un
demi-cylindre en béton, la face arrondie vers le haut.
Ce demi-cylindre a pour rayon 5 cm.
Calcule le volume de béton qui a été utilisé pour construire cette
barrière.
On prendra
![]()
Solutions
1ère partie
Jamais ce bassin sera rempli ! Devine pourquoi.
2ème partie
Je rappelle la formule qui me donne le volume d'un cylindre de rayon à la base R et de hauteur h :
![]()
Le volume
devant être exprimé en dm, je convertis la hauteur
en dm :
30 cm = 3 dm.
Le volume
de ce cylindre, en appliquant la formule précitée est de :
(3,1416 x 0,82 x 3) dm3
= (3,1416 x 0,64 x 3) dm3 = 6,031872 dm3 . Ce volume
vaut donc, au millième par excès, 6,032 dm3 .
3ème partie
Je rappelle d'abord les formules qui seront utilisées dans cet exercice :
Volume d'un parallélépipède
rectangle de base l, L et de hauteur h : L x l x h
Volume d'un cylindre de rayon R et de hauteur (ou génératrice) h :
![]()
Je calcule
le volume du parallélépipède qui vaut
(20 x 10 x 25 ) cm3 = 5000
cm3 .
Ensuite je calcule le volume du demi-cylindre qui vaut :
![]()
Le volume total du béton utilisé dans la
construction de cette barrière sera donc
(5000 + 785,4) cm3
= 5785,4 cm3
un peu de Thalès, de
Pythagore et de trigonométrie
(groupe ciblé : quatrième)
1ère partie
On nous donne un segment
qui mesure 13 cm. On nous demande de le partager par une construction
géométrique (avec la règle et le compas uniquement) en 7parties égales.
Comment fait-on ?
2ème partie
Soit un triangle (MNP) tel
que |MN| = 13 cm, |MP| = 12 cm et |NP| = 5 cm.
Soit E le point de [MN] tel que |ME| = 6 cm.
le cercle de diamètre [ME] coupe (MP) en F.
1- Construis la figure;
2- Démontre que (MNP) est un triangle rectangle;
3- démontre que (MFE) est
également un triangle rectangle, puis démontre que les
droites (FE) et (NP) sont parallèles;
4- Calcule |MF| et |EF|.
3ème partie
Dans une journée d'été et vers 15h on constate que le point O de l'ombre d'un arbre géant, représentant son sommet, se situe à une distance de 5,50 mètres environ du pied (le sol est supposé à cet endroit horizontal, et l'arbre, vertical).
On a pu calculer l'angle que fait l'axe de cette ombre avec la ligne qui joint O au sommet de cet arbre et on a trouvé 65°.
Comment fait-on pour déduire la hauteur approximative de cet arbre.
Solutions
Pour découvrir la solution, ouvre l'animation 10.
2ème
partie
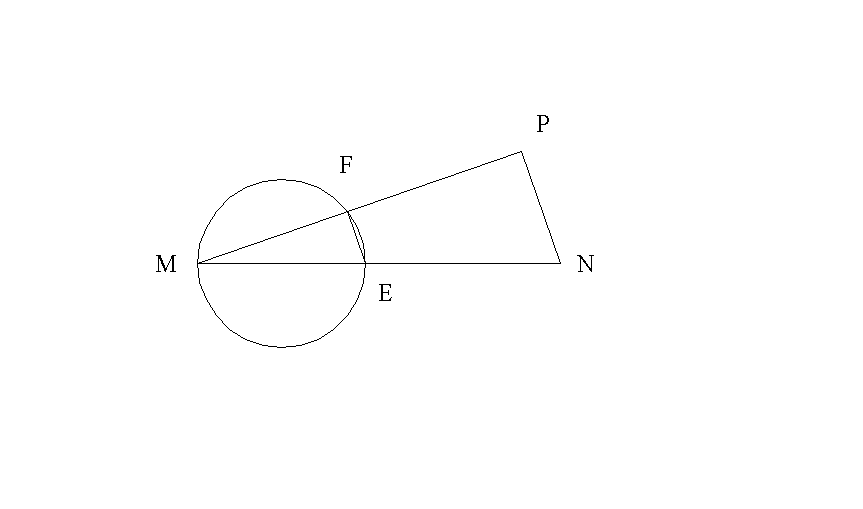
1- Construction de la figure.
Nous devons d'abord vérifier que le triangle
(MNP) est bien constructible. Pour s'y faire, nous montrons que les mesures géométriques des côtés vérifient l'inégalité triangulaire, c'est-à-dire
par exemple :
|MP| - |PN| < |MN| < |MP| + |PN|.
C'est bien le cas puisque 12 - 5 < 13 < 12 +5.
Cette vérification faite, traçons avec la
règle (graduée) le segment [MN] de mesure géométrique 13 cm.
Du point M et avec une ouverture de compas égale à 12 cm traçons un arc de
cercle (L1), puis du point N, avec une ouverture de compas égale à 5 cm traçons un arc de
cercle (L2).
L'intersection de (L1) et (L2) sera le troisième sommet P
de ce triangle.
2- Nous avons 132 = 169 = 122
+ 52 .
Autrement dit, MN2 = MP2 + PN2
.
Le triangle (MNP) vérifiant ainsi la réciproque du théorème de
Pythagore est un triangle rectangle en P.
3- L'angle au sommet F du triangle (MFE) est
inscrit dans le demi-cercle de diamètre [ME].
De plus il intercepte ce diamètre.
En conséquence, il est droit et le triangle (MFE) est rectangle en F.
L'angle en F du triangle (MFE) étant droit, (EF)
est perpendiculaire à (MP).
L'angle en P du triangle (MNP) étant droit, (NP) est perpendiculaire à (MP).
Ainsi (EF) et (NP), du plan du triangle (MNP), étant perpendiculaires à une
même droite (MP), sont parallèles.
4- Dans le triangle (MNP), le segment [EF] est parallèle au côté [NP]. D'après le théorème de Thalès, nous avons :
![]()
D'où nous tirons :
![]()
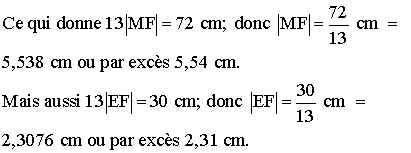
3ème
partie
Soit S le sommet de l'arbre et H représentant le centre de son tronc, au niveau de son pied.
Comme par hypothèse le sol est horizontal, et l'arbre, vertical, le triangle (OHS) est rectangle en H.
Nous avons donc le relation : |OH| = |OS| cos 65°.
D'après le théorème de Pythagore, |OS|2 = |OH|2 + |HS|2 .

d'où en remplaçant dans la
seconde relation :
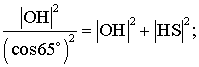
ce qui implique que
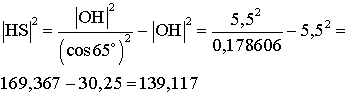
D'où finalement |HS| vaut environ 11,79 mètres.
droites,
application linéaire, application affine et système d'équations
(groupe ciblé : troisième)
Première
partie
![]()
(unité : cm)
1- Trouve une application affine h telle que h(1) = 2 et h(3) = -1;
2- Trouve une application constante t telle que t(1) = -5;
3-
Trouvons l'équation de la droite (d) passant par le point
A (2 ; -1) et parallèle à la droite
(d') d'équation 3x - y = 2.
Deuxième
partie
![]()
(unité : cm)
On donne dans ce repère deux points A (0 ; 4) et B (6 ; 0).
Calcule les coordonnées du milieu I de [AB].
Détermine l'équation de la droite (AB), puis celle de sa médiatrice (D).
Troisième
partie
Résous le système :
2x
+ y = 8
10x + 20y = 7
Quatrième
partie
1- Résous le système suivant où x et y sont les inconnues :
x2
+ 2x -3 = y
y = x + 3
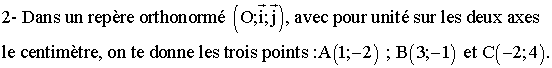
Trouve
les équations des droites (AB), (BC) et (AC).
Calcule les coordonnées de l'orthocentre H du triangle (ABC), celles de son
centre de gravité G, ainsi que celles du centre M de son cercle circonscrit.
Que peux-tu en conclure ?
Solutions
Première
partie
1- Trouvons une application affine h telle que h(1) = 2 et h(3) = -1.
La forme générale de l'équation d'une application affine est y = h(x) = ax + b, avec a et b différents de 0.
Ainsi h(1) = a(1) + b = 2 et h(3) = a(3) + b = -1; d'où le système à résoudre :
a
+ b = 2
3a + b = -1
a
+ b = 2 donne b = 2 - a; en remplaçant dans la seconde équation b par son
égal 2 - a, on obtient :
![]()
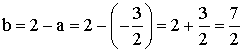
L' application linéaire h sera donc :
![]()
2- Trouvons l'application constante t telle que t(1) = -5.
t devant être une application constante, sa valeur t(x), pour tout nombre x, devra être égale à -5; donc l'application t est t(x) = -5.
3-
Trouvons l'équation de la droite (d) passant par le point
A (2 ; -1) et parallèle à la droite
(d') d'équation 3x - y = 2.
Le
coefficient directeur de (d') est 3 puisque son équation est
y = 3x - 2.
La forme générale de l'équation de (d) est y = ax + b.
Comme (d) devra être parallèle à (d'), son coefficient directeur a devra vérifier l'égalité 3 = a.
De plus (d) devant passer par le point A, les coordonnées de ce point devront vérifier l'équation de (d), donc : yA = 3xA + b.
D'où b = yA - 3xA = -1 - 3(2) = -7
L'équation de (d) sera finalement : y = 3x -7.
Deuxième
partie
Deux points A et B quelconques étant donnés dans le plan du repère, les formules générales donnant les coordonnées xM et yM du milieu M du segment [AB] sont les suivantes :
![]()
Dans le cas de notre exercice, nous avons donc :
![]()
Déterminons
l'équation de la droite (AB), puis celle de sa médiatrice (D).
La
forme générale de l'équation de (AB) étant y = ax + b, et comme les
coordonnées
de A et B doivent vérifier cette équation (puisque A et B appartiennent à
(AB)),
nous avons le système :
yA = axA + b
yB = axB + b
D'où
4
= 0a + b
0 = 6a = b
La
première équation donne directement b = 4 et en remplaçant la valeur 4 de b
dans la seconde équation, on obtient :
![]()
L'équation
de (AB) est donc :
![]()
(D) étant la médiatrice de (AB), elle doit simultanément contenir le milieu I de [AB] et être perpendiculaire à (AB). Donc si son équation est de la forme y = mx +n, on doit avoir :
![]()
2
= 3m + n et la seconde équation donne directement la valeur de m
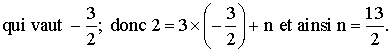
L'équation de (D) sera donc :
![]()
Troisième partie
Le système est :
2x
+ y = 8
10x + 20y = 7
La
première équation donne y = 8 - 2x, et en remplaçant dans la seconde y
par 8 - 2x on obtient :
10x + 20(8 - 2x) = 7; ce qui donne -30x = 7 - 160 = -153;
![]()
y = 8 - 2x = 8 - 2(5,1) = 8 - 10,2 = -2,2.
Quatrième
partie
1- Résolvons le système suivant où x et y sont les inconnues :
x2
+ 2x -3 = y
y = x + 3
La difficulté ici est de pouvoir factoriser l'expression x2 + 2x -3.
Supposons x2 + 2x le début d'un carré de la forme (x + a)2 , donc avec 2ax = 2x; ce qui donne a = 1 et donc x2 + 2x = (x + 1)2 - 1.
Dans
l'expression x2 + 2x -3 remplaçons x2 + 2x par son égal
(x + 1)2 - 1; nous obtenons
(x + 1)2 - 1 -3 qui vaut donc (x + 1)2 - 4 et qui peut
être factorisée puisqu'elle est la différence de deux carrées.
x2 + 2x -3 = y devient donc (x + 1)2 - 4 = y ou encore
(x
- 1)(x + 3) = y.
Le système devient :
(x
- 1)(x + 3) = y
y = x + 3
En
remplaçant dans la première équation y par x + 3, on obtient :
(x - 1)(x + 3) = x + 3.
Amenons tout au premier membre : (x - 1)(x + 3) - (x + 3) = 0.
Factorisons
le premier membre : (x + 3)(x - 1- 1) = 0 ou encore
(x + 3)(x - 2) = 0.
Pour
qu'un produit de deux facteurs soit nul il faut et il suffit que l'un au moins
des deux facteurs le soit. Donc (x + 3)(x - 2) = 0 donne x + 3 = 0 ou x - 2 = 0.
Ainsi x = - 3 ou x = 2.
Pour
calculer y remplaçons dans y = x + 3, x par sa valeur trouvée.
Ainsi, pour x = - 3, y = - 3 + 3 = 0 ou pour x = 2, y = 2 + 3 = 5.
L'ensemble des solutions du système est donc {(- 3 ; 0) ; (2 ; 5)}.
Recommandations
Quatrième
partie - 2
La
seule difficulté dans cet exercice réside dans la conclusion quant au
positionnement des points G, H et M.
Après avoir calculé leurs coordonnées, il faudra trouver par exemple
l'équation de (GH) et d'en déduire la position de M par rapport à (GH).
Nous devons conclure que les trois points G, H, M sont alignés.