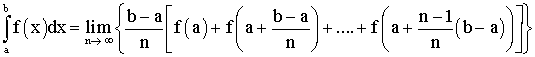
(groupes ciblés : terminales , toutes séries confondues)
les thèmes abordés dans cette page
intégrale et limite d'une suite
(terminale S)
axe
radical
(première et terminale S)
congruences (modulo n) dans Z
(terminale S)
encadrement d'une racine d'une équation -
logarithme
(terminale L)
analyse combinatoire
(terminales)
dérivation et extremums d'une fonction
numérique
(terminales)
extremums
d'une fonction numérique et géométrie
(terminales S et technologiques)
étude d'une fonction numérique et
dérivation
(terminale L)
homothétie et somme
(terminale S)
un peu de cinématique
(terminales S et technologiques)
de la métrique dans
un triangle
(terminale S)
intégrale et limite d'une suite
(groupe ciblé : terminale S)
Soit f une fonction réelle d'une variable réelle intégrable sur [a , b] .
Tu vas admettre l'égalité importante suivante :
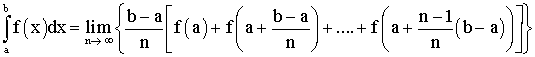
Trouve la limite , lorsque n tend vers l'infini (n étant un entier naturel quelconque différent de 0) , de la suite définie par :
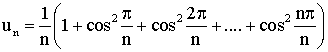
Trouve la limite , lorsque n tend vers l'infini
(n étant un entier naturel quelconque différent de 0) , de la suite définie par :
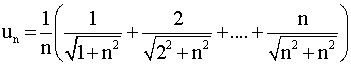
D'abord je te rappelle qu'une suite réelle est
une application d'une partie I de N dans R (généralement I est
égale à N ou N*) .
Ainsi , si tu notes A cette application , pour
tout n élément de I , l'image de n par A , notée A(n) , peut être également
notée : un ,
avec un réel .
L'expression A(n) définissant la suite peut être donnée en fonction
de n ou
en fonction de termes précédents A(n-1) ; A(n-2) ; etc.
La suite correspondante sera notée :
![]()
Ensuite essaie d'interpréter géométriquement
l'égalité importante donnée au début des travaux précités .
Tu
t'apercevras qu'elle n'est pas aussi difficile que tu le croyais .
Pour trouver les limites demandées des suites
données ci - dessus , évidemment il faudra que tu appliques cette égalité fondamentale
.
Pour cela , il te faudra trouver
d'abord qu'elle est la fonction intégrable sur un certain intervalle à
déterminer également ; ceci bien sûr à partir de l'expression donnée de
chacune de ces suites .
Pour t'aider la fonction intégrable est f(x) = cos2 x , pour la première suite ; celle tirée de la seconde suite est :
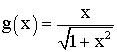
A toi de jouer maintenant .
un théorème
(groupes ciblés : terminales toutes séries scientifiques
confondues)
Rappel
Dans un plan, soit un cercle (C) de centre O et
de rayon r .
Soit un point M quelconque .
On appelle puissance de M par rapport au cercle (C) et on la note P(C)
(M), l'expression :
d2 - r2 .
Dans un plan, on appelle axe radical de
deux cercles quelconques (C); (C'), l'ensemble des points M ayant même
puissance par rapport à ces deux cercles; c'est-à-dire :
P(C) (M) = P(C')
(M) .
Tu peux facilement montrer que cet ensemble est bien une droite perpendiculaire
à la ligne des centres de (C) et (C') .
Tu vas maintenant démontrer le théorème
suivant :
L'intersection des diagonales d'un trapèze appartient à l'axe radical des
deux cercles construits sur les côtés non parallèles .
C'est le théorème de Richa .
Soit le trapèze (ABCD) dont les côtés
parallèles sont [AB] et [CD] .
On pose AB = a ; CD = b .
O et O' sont respectivement les milieux de [AD] et [BC] ; on pose 2r = AD
et 2r' = BC ; on suppose r' strictement supérieure à r .
Soient I l'intersection des diagonales, M le milieu de la base
moyenne [OO'] .
![]()
Trouve l'abscisse xi de la projection orthogonale i de I sur (OO') .
![]()
pour que (ABCD) soit un trapèze isocèle ?
Sachant que
![]()
quelle est alors la position de i sur (OO') ?
congruences (modulo n) dans Z
(groupe ciblé : terminale S)
Construis les tables d'addition et de multiplication sur Z/5 .
Résous dans Z/5 les équations suivantes :
![]()
a et b désignant des éléments de
Z/5 ,
discuter dans Z/5 les deux équations :
![]()
Dans cet exercice tu utiliseras les propriétés du groupe additif (Z ; +) et du groupe multiplicatif (Z* ; .) .
Rappel : dans un ensemble A muni d'une loi de
composition
interne o , on dira que A possède la structure de groupe pour
cette
loi si et seulement si :
- pour tous x , y , z éléments de A , (xoy)oz =
xo(yoz) ;
on dira que la loi o est associative dans A ;
- il existe un élément e de A tel que pour tout x de A
xoe = eox = x ; on appellera
e élément neutre pour la loi o ;
- pour tout élément x de A , il existe un élément x' de A tel que
xox' = x'ox
= e ; on appellera x' élément symétrique de x
pour la loi o .
Si de plus , la loi de composition interne o est
commutative ; c'est-à-dire si pour tous x ; y de A , xoy = yox , on dira que
le
groupe est commutatif ou abélien .
le groupe A muni de la loi de composition interne o sera noté (A ; o) .
encadrement d'une racine d'une équation -
logarithme
(groupe ciblé : terminale L)
On donne la fonction réelle d'une variable
réelle x définie
par :
![]()
1- Quel est le domaine de définition D de f ?
2- Étudie f sur son domaine et trace sa courbe représentative
![]()
3- Au regard de ce qui a été dit aux questions 1 et 2 , montre que l'équation
:
x + Log x = 0 admet dans D une racine et une seule x0 telle que :
0,5 < x0 < 0,75 .
Tu utiliseras la continuité de f , sa monotonie , ainsi que son changement
de signe dans l'intervalle [0,5 ; 0,75] .
4- Trouve l'équation de la tangente T à C au point de cette dernière
d'abscisse x = e .
5- calcule l'aire de la surface A comprise entre les courbes
x = 0 ; y = 0 ; C
et T .
analyse combinatoire
(groupes ciblés : terminales toutes séries
confondues)
Rappel
Prends un ensemble E de n éléments , n étant
un entier naturel différent de 0 .
On appelle arrangement de ces n éléments p à p (p étant un entier
naturel différent de 0 et largement inférieur à n) , tout assemblage de p de
ces éléments dans un ordre de succession déterminé, noté :
![]()
Il y a n.(n -1).(n - 2).(n - 3).....[(n - (p-1)] arrangements; et cette quantité est notée :
![]()
Ainsi on obtient :
![]()
Exemple : combien peux-tu former de nombres de deux chiffres distincts ?
L'ensemble des chiffres est A = {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}. Je te laisse continuer .
Attention : au nombre d'arrangements trouvé, il faudra soustraire celui des arrangements de la forme 0X , avec X appartenant à A*.
Si p est égal à n, alors les arrangements tels que :
![]()
sont appelés permutations des n éléments
et on désigne leur quantité par Pn .
Ainsi
![]()
Pn se note aussi n! qui se lit
"factorielle n".
Par convention on notera 0! = 1 et ainsi l'expression x! est définie sur N .
Exemple : combien de nombres de dix chiffres distincts peux-tu former avec les dix premiers entiers naturels . Là également, il te faudra soustraire de ce nombre, celui des éléments tels que 0ABCDEFGHI .
Reprends l'expression :
![]()
Multiplie le numérateur et le dénominateur (
égal à 1) de cette expression par :
(n - p).(n - p - 1).(n - p - 2).....3.2.1 et en déduis que :

On appelle "combinaison" de p
éléments pris dans un ensemble de n éléments ( n largement supérieur
à p), tout ensemble que l'on peut former en choisissant p de ces
éléments, l'ordre étant cette fois-ci indifférent .
On la note :
![]()
Deux combinaisons ne diffèrent que si l'un au
moins des éléments figurant dans l'une d'elles n'est pas contenu dans l'autre
.
Il y a donc moins de combinaisons que d'arrangements .
Le nombre des combinaisons, noté :
![]()
est égal à :
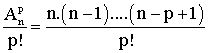
Prends l'expression située au numérateur de la fraction
ci-dessus :
n.(n - 1)....(n - p + 1) .
En multipliant les termes de la fraction :
n.(n - 1)....(n - p + 1) / 1 par (n - p)...1, tu obtiendras l'expression :
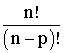
En revenant à l'égalité :
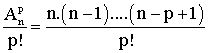
et en remplaçant n.(n -
1)....(n - p + 1) par son égale
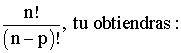
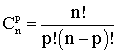
Exemple :
Combien de segments peux-tu former avec 9 points d'un plan , deux à deux
distincts ?
Démontre les deux formules utiles suivantes:
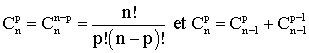
Tu vas , dans la suite , établir le binôme de Newton :
Soit à effectuer le produit suivant :
P = (x + a)n = (x + a).(x + a).(x + a)......(x + a) , n fois .
Un terme s'obtient en choisissant x dans p facteurs (p étant largement inférieur à n) et a dans les (n - p) autres facteurs . Un tel terme est an - p xp .
Il y a autant de tels termes que de choix possibles de p facteurs parmi les n facteurs , sans tenir compte de l'ordre ; quel est alors le nombre de termes de la forme : an - p xp ?
Ainsi , tu obtiens :

Calcule
![]()
Tu trouveras que ces deux quantités sont égales à 1
D'où
![]()
Comme
![]()
tu obtiens :
![]()
C'est finalement le binôme de Newton .
Il peut s'écrire :
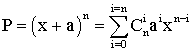
Les quantités telles que :
![]()
sont appelées coefficients du binôme de Newton .
Tu peux facilement démontrer le théorème
suivant :
les coefficients du binôme de Newton équidistants des termes extrêmes sont égaux .
A partir des conclusions ci-dessus , tu peux
facilement construire
ce qu'on appelle " triangle de Pascal " ; à toi de jouer .
(groupes ciblés : terminales scientifiques)
La démonstration du binôme de Newton a supposé que les éléments x et a appartiennent à tout anneau devant vérifier un condition importante ; laquelle ?
En particulier , la formule correspondante s'applique également pour x et a appartenant à l'ensemble C des nombres complexes .
Quelques exercices
(groupes ciblés : terminales toutes séries confondues)
1) On considère un jeu de 32 cartes . On veut former des paquets de 5 cartes comprenant 4 cartes de même nom (4 as ou 4 rois , etc.) ; combien peut-on former de tels paquets ?
2) Combien y a-t-il de diagonales dans un polygone de n côtés ?
3) p est un entier naturel donné ; x et y des
entiers naturels inconnus .
Combien l'équation x + y = p admet-elle de
solutions ?
4) Une assemblée contient 20 personnes . On veut
constituer un bureau comportant un président , un secrétaire et un trésorier
.
Combien y a-t-il de façons de constituer le bureau ?
5) Dans l'alphabet il y a 26 lettres dont 6
voyelles .
Combien peut-on former de mots de 3 lettres avec deux consonnes différentes
et une voyelle , la voyelle occupant le second rang ?
6) La classe d'une institutrice est composée de 18 élèves . Combien peut-elle former des groupes de 4 élèves ?
7) On donne n points de l'espace deux à deux
distincts .
Combien peut-on tracer de droites joignant ces n points ?
Combien peut-on construire de vecteurs ayant toutes leurs extrémités choisies
parmi ces n points ?
8) Écris le développement de (x + a)n
.
En faisant x = a = 1 , calcule :
![]()
En faisant x = -a = 1, calcule :
![]()
En déduire la somme des coefficients de rang pair , ainsi que celle des coefficients de rang impair .
9) On considère les nombres de 5 chiffres
formés avec les 5 chiffres distincts :
1 , 2 3 , 4 , 5 .
Combien y a-t-il de nombres formés avec les 5 chiffres distincts précédents ?
Quelle est la somme de ces nombres ?
10) Écris le développement de (x + a)n .
En dérivant par rapport à x l'égalité
précédente , montre
que :
![]()
En intégrant , en déduire les valeurs respectives des quantités suivantes :
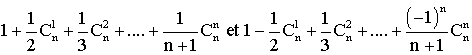
(groupe ciblé : terminale S)
1) En développant (1 + z)n par la formule du binôme de Newton puis en remplaçant z par les racines cubiques imaginaires de l'unité , calcule les sommes :
![]()
2) tu poseras :
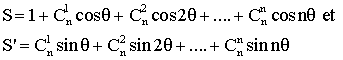
Forme S + iS' et en déduis S et S' .
dérivation et extremums d'une fonction
numérique
(groupes ciblés : terminales toutes séries
confondues)
1- Démontre que si le polynôme f(x) est
divisible par
(x - a)2 , sa dérivée f'(x) est divisible par (x - a)
et que, réciproquement, si un polynôme f(x) divisible par (x - a), a une
dérivée, elle-même divisible par (x -a), f(x) est divisible par (x - a)2
.
2- En déduire que, pour que l'équation f(x) =
0, dans laquelle f(x) est un polynôme, ait une racine double (c'est-à-dire
deux racines égales), il faut et il suffit que les deux équations :
f(x) = 0 et f'(x) = 0 aient une racine commune .
Dans tout ce qui suit, tu prendras un repère orthonormé .
3- Détermine a de façon que la courbe y = x3 - ax2 + 1 soit tangente à la droite y = 5 et construis la courbe correspondante .
4- La droite y = 5 rencontre la courbe précédente en un point A et la rencontre à nouveau au point B dont tu calculeras l'abscisse .
5- Chaque courbe y = x3 - ax2
+ 1 a un maximum et un minimum ; peux- tu le démontrer ?
On te demande de déterminer ensuite les ensembles décrits par ce maximum et ce
minimum quand le réel a varie .
une partie de billard
(groupe ciblé : terminales scientifique et
technologique)
Un billard rectangulaire (ABCD) a pour dimensions
AB = DC = a,
AD = BC = b > a . Une bille part de A et frappe successivement
les bandes [BC], [CD], [DA], en des points M, N, P .
Elle s'arrête après avoir bouclé un quadrilatère (MNPQ) .
L'angle
de réflexion est égal, chaque fois, à l'angle d'incidence .
1- Entre quelles limites doit être compris BM =
x pour que les
bandes soient frappées dans cet ordre ?
Quelle est alors la
forme du quadrilatère (MNPQ) ?
Montre que les droites supportant les côtés,
ou la diagonale
[MP], passent chacune par un point fixe .
2- Calcule en fonction de x l'aire de ce
quadrilatère .
Dans un repère orthonormé, construis le graphe de la fonction
:
![]()
Deux des circonstances suivantes peuvent-elles se
produire simultanément :
(MNPQ) rectangle, (MNPQ) losange, (MNPQ) d'aire
maximum ?
3- Calcule en fonction de l'angle BAM = t la
longueur z de la ligne brisée [AMNPQ] parcourue par la bille depuis son départ
A jusqu'à son point d'arrêt Q .

Quels sont, dans cet intervalle, les extremums de z ?
étude d'une fonction numérique et
dérivation
(groupe ciblé : terminale L)
Étudie les variations de la fonction numérique f définie par :
![]()
Représente sa courbe (C) dans un repère orthonormé et calcule l'aire comprise
entre (C) et les deux droites d'équation x = -2 et x = -1 .
homothétie et somme
(groupe ciblé : terminale S)
1- Étudie le variations de la fonction :
f(x) = 4x3 - 3x + 1
Construis le graphe (C) de f dans un repère orthonormé et montre que (C) possède un centre de symétrie .
2- Calcule l'aire comprise entre l'axe des abscisses, celui des ordonnées et l'arc de (C) sur lequel x varie de 0 à 0,5 .
3- Montre que le graphe de la fonction :
![]()
où l
est un réel
constant, se déduit de (C) par homothétie .
Quel est, lorsque l varie,
l'ensemble des points de cette courbe qui correspondent à un maximum de g(x) et
quel est l'ensemble des
points qui correspondent à un minimum ?
4- Étudie les variations de la fonction :
![]()
Construis sa courbe représentative et indique quelles sont les tangentes à cette courbe aux points qui ont pour abscisses -1 et 0,5 .
5- Calcule cos 3f en
fonction de cos f.
Tu utiliseras la relation obtenue
et le changement x = cos f
pour trouver les racines de l'équation :
![]()
exponentielle
(groupes ciblés : terminales toutes séries
confondues)
Calcule la dérivée de la fonction numérique : y = (n - x) ex , où n est une constante réelle .
Étudie, quand x est un réel largement positif,
les variations de la fonction : y = (2 - x) ex
et en construis la courbe représentative
pour
ces valeurs de x dans un repère orthonormé .
Calcule l'aire du domaine compris entre cette
courbe et les
demi-axes [Ox et [Oy .
un peu de cinématique
(groupes ciblés : terminales S
et techno.)
1- calcule la dérivée de e-x .
![]()
les coordonnées d'un point M sont données
en fonction
de l'instant t par les formules :
x = et , y = e-t , où t prend toute valeur réelle .
Construis la trajectoire, (C), du point M .
3- Donne les coordonnées du vecteur-vitesse et
du
vecteur-accélération du point M à l'instant t .
![]()
vecteur-vitesse de M à l'instant t; construis la courbe (H) décrite
par m;
compare (H) et (C) .
5- On considère sur (C) le point M à un instant
quelconque t;
![]()
que M' est sur (Ox) .
![]()
un peu de la métrique dans
un triangle
(groupes ciblés : première et terminale S)
On te donne dans un plan fixe deux points
distincts et fixes E et F. On pose |EF| = a, a réel strictement positif.
Dans ce plan, un point M mobile se déplace tel que
ME2 + MF2
= k2 , avec k réel constant dont la valeur absolue est différent de
0.
Trouve le lieu géométrique de M (c'est-à-dire la trajectoire que décrit M ou encore
l'ensemble des points M), en te servant de la notion de produit scalaire.
Pour t'aider dans ton raisonnement, ouvre la page animation 2.
tu as dis ellipse ?
(groupe ciblé : terminale S)
Première partie : la notion fondamentale de l'ellipse.
On te donne dans un plan fixe deux points
distincts et fixes A et B.
Un point M mobile de ce plan se déplace tel que |MA| + |MB| = k, k étant une
constante réelle strictement positive.
Trouve le lieu géométrique du point M.
Pour t'aider dans ton raisonnement, ouvre la page animation 3.
Deuxième partie : une autre définition de l'ellipse.
On te donne dans un plan fixe une droite (d') fixe et un point A fixe n'appartenant pas à (d').
Un point M de ce plan se déplace tel que le rapport de |MA| à |MH|, H étant la projection orthogonale de M sur (d'), soit égal à une constante réelle k tel que 0 < k < 1.
Trouve le lieu géométrique du point M.
Pour t'aider dans ton raisonnement, ouvre la page:
Troisième partie : transformé d'un cercle par affinité orthogonale.
On te donne dans un plan fixe un cercle quelconque de diamètre fixe [AB].
Trouve le transformé de ce cercle par l'affinité orthogonale d'axe (AB), la droite support de [AB], et de rapport constant le réel k, |k| étant différente de 0 et de 1.
Pour t'aider dans ta recherche, ouvre la page animation 5.
une petite révision à nos L
(groupe ciblé : terminale L)
Première partie
Un sac contient 12 boules blanches et 8 boules rouges. Tu tires 4 boules de ce sac.
1) Quel est le nombre de cas possibles ?
2) Quel est le nombres de cas favorables à l'obtention de 3 boules blanches et une boule rouge ? En déduire la probabilité correspondante.
Deuxième partie
Soit l'équation dont l'inconnue est x et où m est un paramètre réel, définie par :
![]()
On te
demande de résoudre graphiquement cette équation, en fonction des valeurs
que peut prendre m.
Représente graphiquement la fonction numérique g définie par :
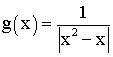
Dans cette partie le repère sera orthonormé.
Troisième partie
Quelle est la nature de la suite des fractions :
![]()
Vers quelle limite tend la somme des termes de cette suite infinie de fractions ?
Quatrième partie
Résous dans R2 le système suivant :
x + y = 65
log x + log y = 3
Je te rappelle que le symbole log (avec un "l" minuscule) est celui des logarithmes décimaux.