L'ATELIER DU LYCÉEN
(page 1)
(groupes ciblés : seconde et premières , toutes séries confondues)
les thèmes abordés dans cette page
fonction réelle d'une variable réelle -
généralités
(seconde)
puissances d'un nombre et géométrie
(seconde)
parallélogramme et extremum d'une parabole
(seconde et première S)
système d'inéquations du premier degré et
étude des angles intérieurs d'un triangle
(seconde)
droites et plans parallèles
(première S)
la géométrie analytique dans l'espace à
trois dimensions
(premières et terminales)
un peu de trigonométrie
(premières S et technologiques)
puissance d'un point par rapport à un cercle
et axes radicaux de deux cercles
(première S)
une transformation trigonométrique
(premières)
fonction réelle d'une variable réelle -
généralités
(groupe ciblé : seconde)
![]()

R peut être représenté par une droite
dite droite réelle , munie d'une origine O ![]()
![]()
Prends un point quelconque M sur cette droite .
![]()
Par définition le
réel k est dit abscisse du point M .
Un intervalle fermé , noté [ab] , est la partie de R telle que :
![]()
Un intervalle ouvert , noté ]ab[ , est la partie de R
telle que :
![]()
Un intervalle semi - fermé à gauche (ou semi - ouvert à droite) , noté [ab[
, est la partie de R telle que :
![]()
Un intervalle semi - fermé à droite (ou semi - ouvert à gauche) , noté ]ab]
, est la partie de R telle que :
![]()
Une fonction réelle d'une variable réelle ,
notée par exemple f , est une
relation dans R qui à tout réel x ,
appelé variable réelle , associe au plus un
réel y appelé image de x par f .
On écrit alors : y = f(x)
.
Notons dans ce cas qu'un élément x de R peut ne pas avoir d'image par f . Mais si l'image de x par f existe alors elle est unique .
On appelle domaine de définition de f la partie de R formée de tous les réels ayant une image par f . Elle sera notée dom (f) .
![]()
0 n'a pas d'image par f dans R ; nous dirons que f n'est pas définie pour x = 0 .
dom (f) = R* .
Soit f une fonction réelle d'une variable
réelle définie sur un intervalle I inclus
dans R , I pouvant être
fermé , semi - fermé ou ouvert .
On dira que f est largement croissante sur I si , pour tous x1 , x2 de I tels que x1 différent de x2 on a :
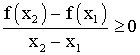
On dira que f est largement décroissante sur I si , pour tous x1 , x2 de I tels que x1 différent de x2 on a :
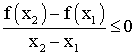
On dira que f est strictement croissante (resp.
strictement décroissante) sur I si , pour tous
x1 , x2 de I tels que x1 différent de x2
on a :
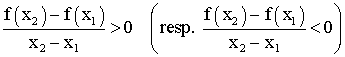
On dira que f est constante sur I si , pour tous x1 , x2 de I tels que x1 différent de x2 on a :
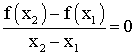
On dira que f est monotone sur I si elle est croissante ou décroissante sur I . Elle sera dite largement monotone sur I si elle est largement croissante ou largement décroissante sur I ; elle sera dite strictement monotone sur I si elle est strictement croissante ou strictement décroissante sur I .
Soit f une fonction numérique définie sur un
ensemble D inclus dans R .
On dira que f admet un maximum en un point x0
appartenant à D ,
si et seulement si , pour tout x appartenant à D ,
![]()
La valeur f(x0
) sera appelée maximum de f sur D .
On dira que f admet un minimum en un point x1 appartenant à D , si
et
seulement si , pour tout x appartenant à D ,
![]()
La valeur f(x1) sera appelée
minimum de f sur D .
f sera dite bornée supérieurement sur D s'il
existe un réel k tel que :
pour tout x appartenant à D ,
![]()
f sera dite bornée inférieurement sur D s'il existe un réel h
tel que :
pour tout x appartenant à D ,
![]()
k et h seront appelés respectivement borne supérieure et borne inférieure
de
f sur D .
R2
étant l'ensemble des couples (x , y) de réels , prenons dans son plan
représentatif deux droites d et d' n'ayant pas le même support et se
coupant en O .
Portons R sur d et sur d' et munissons chacune de ces dernières d'un
vecteur unitaire :
![]()
![]()
![]()
Dans le plan R2 le couple (x'x , y'y) sera appelé repère et
on dira que le plan est ramené
à son repère . L'axe x'x sera dit axe des
abscisses et l'autre , y'y , sera appelé axe des ordonnées .
A tout point du repère correspond un couple (x , y) de R2 et
un seul , et réciproquement .
x sera dit abscisse de ce point et y , son ordonnée .
Le
repère sera dit quelconque si les vecteurs unitaires qui lui sont rattachés
ont des modules (ou normes ou encore longueurs géométriques) différents et
si l'angle formé par
ses deux axes est différent de 90 degrés .
Il sera dit normé si les deux vecteurs unitaires ont le même module (ou norme)
, l'angle formé par ses deux axes étant encore différent de 90 degrés .
Il sera dit orthogonal si l'angle formé par ses deux axes est égal à 90
degrés et les deux vecteurs unitaires de normes différentes.
Il sera dit orthonormé (ou orthonormal) si l'angle formé par ses deux
axes est égal à 90 degrés et si les deux vecteurs unitaires ont de normes égales .
![]()
Soit une f une fonction réelle d'une variable réelle .
A tout élément x de son domaine correspond un
réel y et un seul et on
écrit y = f(x) .
Ainsi le couple (x , f(x)) peut être
représenté dans le repère précédemment défini par un point M .
Donc lorsque
x décrit dom(f) , y décrit un sous ensemble de R et le point M décrit
une certaine courbe dans le repère . Cette courbe sera appelée représentation
graphique (ou courbe représentative) de f dans le repère considéré .
En
vue de la représentation graphique de f , on aura besoin d'établir son tableau
de variations qui n'est qu'un tableau à double entrée , dans lequel on prendra
sur les colonnes des valeurs assignées à la variable x et sur la ligne ,
les images correspondantes .
Les valeurs qu'on assigne à la variable x sont généralement choisies en
fonction de leur pertinence au regard de l'étude faite sur la fonction ; par
exemple on retiendra les valeurs de x qui annulent f ou qui la rend maximale
ou minimale .
Dans
un repère orthogonal , la fonction réelle d'une variable réelle f admet pour
axe de symétrie l'axe y'y des ordonnées si pour tout x appartenant à dom(f) ,
f(x) = f(-x) .
De plus f sera dite fonction paire .
Dans un repère normé , elle admet pour centre de symétrie l'origine O du
repère si f(-x) = -f(x) . De plus f sera dite fonction impaire .
Méthodologie
pour l'étude d'une fonction réelle d'une variable réelle f :
1) On détermine d'abord le domaine de définition de f ;
2) on vérifie ensuite sa monotonie et , le cas échéant , on vérifie si elle
est maximale ou minimale sur son domaine de définition et on détermine dans ce
cas le maximum ou le minimum ;
3) on détermine ensuite les valeurs de x pertinentes au regard de l'étude de f
(les valeurs qui annulent f , les valeurs pour lesquelles f est maximum ou minimum , etc) ;
4) on vérifie si la courbe représentative de f admet l'axe des ordonnées pour
axe de
symétrie (repère orthogonal ou orthonormé) ou l'origine O pour centre de symétrie (repère normé ou orthonormé) ; autrement dit on vérifie si f est paire ou
impaire .
5) enfin on trace à l'aide des résultats obtenus précédemment sa courbe
représentative .
1ère
application
Soient les fonctions suivantes :
![]()
![]()
Détermine dom(f) et dom(g) .
2ème application
On donne la fonction numérique f suivante : f(x) = x2 - | x - 1| .
Étudie f sur l'intervalle [-2 , 2] et trace sa courbe représentative dans un repère orthonormé .
3ème application
Montre que la courbe représentative de h(x) = - x2 admet pour axe de
symétrie l'axe des ordonnées .
Montre que la courbe représentative de k(t) = t3 admet pour centre
de symétrie l'origine O du repère .
NB : tu prendras dans les deux cas comme repère un repère orthonormé .
4ème application
Étudie sur l'intervalle [-3 , 3] la fonction f définie par :
![]()
Représente graphiquement f dans un repère
orthonormé .
Étudie graphiquement l'existence des racines de l'équation f(x) = m où
m est un paramètre réel , et ceci sur l'intervalle [-3 , 3]
.
puissances d'un nombre et géométrie
(groupe ciblé : seconde)
1) Trouve un procédé géométrique pour construire le segment [AB] de longueur :
![]()
Calcule les réels x et y pour satisfaire l'égalité suivante :
![]()
En déduire une construction géométrique du segment [CD] de longueur, en centimètres, égale à :
![]()
2) On te donne un triangle rectangle (ABC)
rectangle en A . Soit (AH) la hauteur relative à l'hypoténuse .
Démontre la similitude des triangles (ABH) et (ACH) et en déduis que
AH2 = HB.HC
![]()
deux axes est le centimètre , les
points A (1 ; 0) et M (0 ; a) ,
a étant un réel strictement positif .
Soient les points P , Q , R ; P appartient à x'x et (MP) est perpendiculaire à
(AM) , Q appartient à y'y et (PQ) est perpendiculaire à (MP) , R appartient à
x'x et (QR) est perpendiculaire à (PQ) .
Détermine les abscisses des points P
et R ainsi que l'ordonnée de Q .
Que peux-tu en déduire pour |xP | ; |yQ | ; |xR
| ?
On te donne en centimètres :
![]()
Que valent alors |xP | ; |yQ
| ; |xR | ?
Trouve un procédé géométrique
pour placer les points A , P , Q , R .
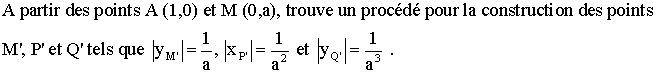
parallélogramme et extremum d'une parabole
(groupes ciblés : seconde et première S)
Que doivent vérifier les réels positifs a , b ,
c pour que le triangle (ABC) tel que
AB = c , BC = a et AC = b soit constructible ?
Soit un point quelconque M appartenant à [AB] et
tel que AM = x .
Quel est le domaine de définition de x ?
Soit h la mesure géométrique de la hauteur [AH]
relative
au côté [BC] .
Mène de M une parallèle à (BC) qui rencontre (AC) en N .
Mène de N une parallèle à (AB) qui rencontre (BC) en P .
Quelle est la nature du quadrilatère (MNPB) ?
Détermine la valeur que doit prendre x pour que l'aire de ce quadrilatère soit
maximale .
La suite de l'exercice est dédiée aux lycéens de première S
Pour la suite de l'exercice tu prendras a = 6 cm
, b = 5 cm
et c = 7 cm .
Calcule la mesure géométrique h de la hauteur [AH] .
![]()
l'aire f(x) du quadrilatère (MNPB) .
L'unité prise sur les deux axes du
repère est le centimètre .
On te donne un point Q de (C) tel que xQ = 4 .
Détermine la tangente (d) à (C) au point Q .
Trouve l'équation de la droite (d') passant par Q et faisant avec (d) un angle
(d , d') égal en valeur absolue à 30° .
![]()
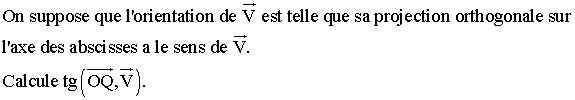
système d'inéquations du premier degré et
étude des angles intérieurs d'un triangle
(groupe ciblé : seconde)
On te donne un triangle quelconque (ABC) dont les
mesures en degré de ses angles intérieurs sont :
a pour l'angle au sommet A ; b pour l'angle au sommet B et c pour l'angle au
sommet C .
De plus tu supposeras :
![]()
Sachant que a + b + c = 180° et que c se déduit
de a et b , tu t'intéresseras uniquement à l'étude de a et b .
Trouve les six conditions que doit vérifier le couple (a ; b) .
Résous graphiquement le système qui découle de
ces six conditions .
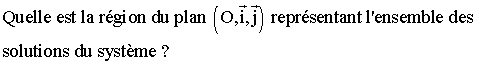
Quel est l'ensemble de points (a ; b) pour lequel le triangle (ABC) n'existe pas ?
Quel est l'ensemble des points (a ; b) pour lequel le triangle (ABC) est isocèle ? équilatéral ? rectangle ? rectangle isocèle ?

droites et plans parallèles
(groupe ciblé : première S)
Rappel des définitions et des théorèmes
Axiome d'Euclide : Existence et unicité de la parallèle à une droite menée d'un point ne lui appartenant pas .
Théorème 1 : Si deux droites sont parallèles, tout plan coupant l'une coupe l'autre .
Théorème 2 : Deux droites x et y parallèles à une même troisième z sont parallèles entre elles .
Théorème 3 et ses conséquences : Deux angles
qui ont les côtés respectivement parallèles et de même sens sont
isométriques.
Deux angles qui ont leurs côtés respectivement parallèles et de sens
contraires sont isométriques .
Deux angles qui ont deux côtés parallèles et de même sens, et les deux
autres parallèles et de sens contraires sont supplémentaires (la somme de
leurs mesures vaut 180°) .
Définition 1 : On appelle angle de deux droites (d) et (d') que l'on note (d ; d'), l'un des angles formés par les parallèles menées d'un point quelconque A de l'espace à ces deux droites . Si l'un de ces angles est droit, alors on dira que (d) et (d') sont orthogonales .
Définition 2 : Une droite (d) et un plan P sont parallèles lorsqu'ils n'ont aucun point commun .
Théorème 4 et ses corollaires : Pour qu'une
droite (d), non contenue dans un plan P, soit parallèle à P, il faut et il
suffit qu'elle soit parallèle à une droite de ce plan .
Lorsqu'une droite (d) est parallèle à un plan P, elle est parallèle à
l'intersection de ce plan avec tout plan Q contenant (d) .
Lorsqu'une droite (d) est parallèle à un plan P, toute parallèle (AB) à (d)
menée d'un point quelconque A de P est contenue dans P .
Théorème 5 : Toute droite parallèle à deux plans sécants est parallèle à leur intersection .
Théorème 6 : Lorsque deux plans sécants P et Q contiennent respectivement deux droites parallèles (y) et (z), leur intersection (d) est parallèle à (y) et à (z) .
Théorème 7 : Par un point donné de l'espace, on peut mener un plan et un seul parallèle à deux droites données non parallèles .
Théorème 8 : Par une droite (d) donnée de l'espace, on peut mener un plan et un seul parallèle à une droite donnée (d') non coplanaire avec (d) .
Définition 3 : Deux plans sont dits parallèles lorsqu'ils n'ont aucun point commun .
Théorème 9 et son corollaire : Pour que deux
plans de l'espace soient parallèles il faut et il suffit que l'un d'eux
contienne deux droites concourantes parallèles
à l'autre .
Deux plans de l'espace sont parallèles lorsque l'un d'eux contient deux droites
concourantes respectivement parallèles à deux droites concourantes de l'autre
.
Théorème 10 et ses corollaires : Par un point
donné A de l'espace, n'appartenant pas à un plan P, on peut mener un plan Q
parallèle à P et un seul .
Deux plans parallèles à un même troisième sont parallèles entre eux .
Lorsque deux plans de l'espace sont parallèles, tout plan qui rencontre l'un
d'eux rencontre aussi l'autre et les deux droites d'intersection sont
parallèles .
Théorème 11 et ses corollaires : L'ensemble des
droites parallèles à un plan P, menées d'un point donné A n'appartenant à
P, est le plan Q passant par A et parallèle à P .
Lorsque deux plans sont parallèles, toute droite qui coupe l'un coupe l'autre;
toute droite parallèle à l'un est parallèle à l'autre .
Théorème 12 : Deux plans parallèles découpent
sur deux droites parallèles des
segments isométriques .
Théorème 13 et sa réciproque : Trois plans parallèles
découpent sur deux droites
qui leur sont sécantes , quelconques, des segments dont les mesures
géométriques sont
proportionnelles . Réciproquement, si trois droites (AA') , (BB') et (CC')
découpent
sur deux droites (d) et (d') non coplanaires des segments dont les
mesures géométriques
sont proportionnelles, ces trois droites sont
contenues dans des plans parallèles .
la géométrie analytique dans l'espace à
trois dimensions
(groupes ciblés : premières et terminales)
Repère orthogonale de l'espace .
Soient dans l'espace trois axes (x'Ox), (y'Oy), (z'Oz) deux à deux orthogonaux
concourant en un point O; les vecteurs unitaires
![]()
On obtient ainsi un repère orthogonale quelconque noté :
![]()
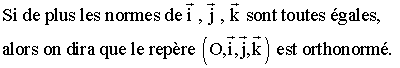

Points et vecteurs de
l'espace à trois dimensions
![]()

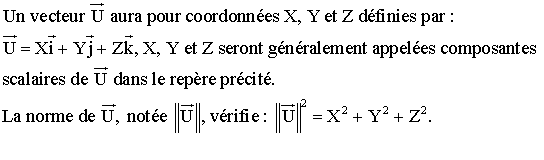
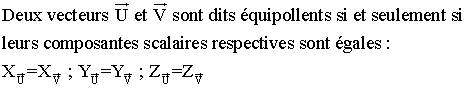

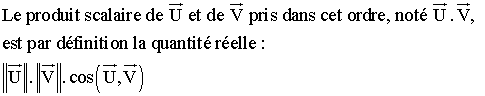

Exercices
1) On te donne un tétraèdre (ABCD) dans lequel
les arêtes [AB] et
[CD] sont orthogonales .
AB = CD = a et BC = b .
Un plan parallèle à (AB) et (CD) rencontre les arêtes [BC] ; [AC] ; [BD] ;
[AD] respectivement en M , N , P , Q .
Montre que le quadrilatère (MNQP) est un
rectangle .
Calcule l'aire de ce rectangle en fonction de a, b et BM = x .
Pour quelle valeur de x cette aire est-elle maximale ?
2) On te donne un plan P et deux droite non
coplanaires (D) et (d) coupant ce plan respectivement en A et B .
Prends un point M variable de (D) . La parallèle à (d) menée de M coupe P en
M' .
Trouve l'ensemble des points M' lorsque M décrit
(D) ;
Le plan P' passant par M et parallèle à P coupe (d) en un point N .
Quelle est
la nature du quadrilatère (MM'BN) ?
Construis le point M lorsque MN est égale à une longueur donnée l .
Discuter .


![]()
distincts A(a; b; c) et B(a'; b'; c') .
Détermine l'équation de la droite (AB) .
Tu montreras ainsi que l'équation
d'une droite de l'espace à trois
![]()
![]()
Si de plus a'-a ; b'-b ; c'-c sont toutes non nulles , tu pourras écrire :
![]()
Cette forme est dite forme canonique de la
droite (AB) . Elle peut se ramener à un système de deux équations du premier
degré également appelées équations canoniques de la droite (AB) .
Par définition le vecteur de composantes scalaires (a'-a) ; (b'-b) ; (c'-c) est appelé vecteur directeur de la droite (AB) . Il est évident que le support ou la direction de ce vecteur est parallèle à (AB) .
On te donne deux points E(1; -2; 3) et F(0; 3; 4) . Écris l'équation de la droite (EF) . Soit une droite (d) passant par le point G(-1; 2; 5) et orthogonale à (EF) . Peux-tu trouver une équation de (d) ? Justifie .
suites numériques
(groupes ciblés : premières toutes séries
confondues)
Étudie la monotonie des suites numériques suivantes :
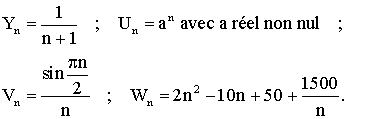
La suite numérique suivante :
![]()
est-elle convergente ?
Étudie la convergence de la suite numérique :
![]()
un peu de trigonométrie
(groupes ciblés : premières scientifique et
technologique)
1- Exprime en fonction de sin x ou de cos x les
expressions
suivantes :
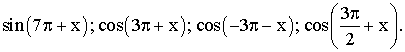
2- Exprime en fonction de tg x ou de cotg x les
expressions
suivantes :
3- Simplifie :
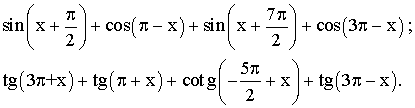
4- Démontre les identités suivantes :
cos4 x - sin4 x + 2 sin2 x = 1 ;
cos4 x - sin4 x - 1 = - 2 sin2 x cos2
x ;
cos6 x + sin6 x - 1 = - 3 sin2 x cos2
x ;
2 cos6 x + 2 sin6 x + 1 = 3 (sin4 x + cos4
x) ;
(tg x + cotg x) sin x cos x = 1 ;
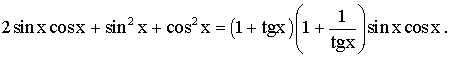
5- Démontre l'énoncé :
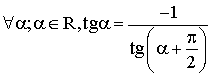
En déduire la relation qui doit lier les pentes de deux droites rectangulaires dans un repère orthonormé .
Que peut-on dire des droites dont les pentes sont
racines
de l'équation :
x2 - (m + 1) x - 1 = 0 ?
6- t étant la variable réelle, trouve la
période de la fonction x suivante :
x = sin t - 3 cos 2t .
Je te rappelle que la fonction x = f(t) est dite périodique de période T,
lorsque : f(t + T) = f(t) , pour tout t , élément du domaine de
définition de f .
puissance d'un point par rapport à un cercle
et
axes radicaux de deux cercles
(groupe ciblé : première S)
Rappel
Dans un plan, la puissance d'un point M par
rapport à un cercle (C)
![]()
Soit (MT) la tangente issue de M à (C) , T
étant le point de tangence . Soit une droite sécante quelconque (d) passant
par M et coupant (C) en P et Q .
![]()
Soient, dans un plan, deux cercles quelconques
(C) et (C') .
On appelle axe radical de (C) et (C') l'ensemble des points M de leur
plan ayant même puissance par rapport à ces deux cercles .
Démontre le théorème suivant :
Dans un trapèze, l'intersection des diagonales appartient à l'axe radical
des deux cercles construits sur ses côtés non parallèles .
C'est le théorème de Richa .
Soit maintenant dans un plan, un trapèze
quelconque (ABCD) de côtés parallèles [AB] et [DC] . On pose AB = a ; DC = b
; AD = d et BC = d' .
Soit M le milieu de la base moyenne .
I étant l'intersection des diagonales, O, O' étant respectivement les milieux
de [AD] et [BC], H étant la projection orthogonale de I
sur la base moyenne,
![]()
une transformation trigonométrique
(groupes ciblés : premières toutes séries confondues)
A tout point M de coordonnées x et y d'un plan rapporté à un repère orthonormé, on associe l'équation :
a cos 2t+x sint+y = 0 (1)
où a est un réel donné et
t la mesure d'un angle inconnu exprimé en radians .
![]()
1- Détermine l'ensemble des points M du plan
pour lesquels l'équation (1) admet une racine double (c'est-à-dire deux
racines égales) ; pour cela tu pourras former l'équation ayant pour inconnue X
= sint .
2- Précise les régions du plan pour lesquelles (1) admet deux racines .