L'ATELIER DU COLLÉGIEN
(page 2)
(groupes ciblés : de la sixième à la
troisième)
les thèmes abordés dans cette page
la
résolution d'une équation
(6ème)
fractions et opérations sur les fractions
(5ème, 4ème et 3ème)
la
résolution d'une équation
(groupe ciblé : sixième)
Une équation est
une égalité dans laquelle figure un nombre inconnu
ou une quantité inconnue.
Une équation est donc composée de deux membres
séparés par le signe de l'égalité =
Le membre situé à gauche du symbole = est souvent appelé premier
membre de l'équation; celui de droite est appelé second
membre.
La quantité inconnue peut figurer soit dans le premier membre, soit dans le
second, soit dans les deux.
Résoudre une équation veut dire trouver par le calcul la ou les valeurs que peut prendre la quantité inconnue; ces valeurs sont également appelées racines ou solutions de l'équation.
Dans une équation, le nombre inconnu peut être représenté
par un objet quelconque : un petit symbole ou encore une lettre.
Souvent cet inconnu est représenté par la lettre x.
Mettre en équation l'énoncé d'un problème veut dire traduire les hypothèses et la question du problème en équation.
Méthode de résolution d'une équation
1- Si j'ajoute une même
quantité aux deux membres d'une
équation, j'obtiens encore une équation.
Exemple :
Soit à résoudre l'équation x - a = b, l'inconnu étant x.
Je remarque qu'en ajoutant a au premier membre, donc x - a + a, j'obtiens x, car
- a + a = 0.
Dans ce cas il faudra également ajouter a au second membre, et j'obtiens donc b
+ a.
Ainsi x - a = b implique que x - a + a = b + a ou x = b + a.
La solution de l'équation est donc la valeur b + a.
2- Si je retranche une même
quantité des deux
membres d'une équation, j'obtiens encore une équation.
Exemple :
Soit l'équation x + m = n, l'inconnu étant x et .
Je remarque qu'en retranchant m des deux membres, j'obtiens la valeur de l'inconnu x.
En effet, x + m - m = n - m
Mais m - m = 0
Donc x = n - m
La solution de l'équation est donc la valeur n - m.
3- Si je multiplie ou je divise par une même quantité différente de 0 les deux membres d'une équation, j'obtiens encore une équation.
Exemple 1
Soit l'équation a × y = d où le nombre inconnu est y et a différent de 0.
Si je divise les deux membres de cette équation
par a, j'obtiens encore une équation et ainsi :
![]()
![]()
![]()
Exemple 2
![]()
Si je multiplie les deux membres de cette
équation par c, j'obtiens encore une équation et ainsi :
![]()
![]()
L'équation
devient :
![]()
4- Conclusion générale
Si par une même transformation T, je transforme les deux membres d'une équation, j'obtiens encore une équation.
Exemple :
![]()
La
transformation T à utiliser est la suivante : «
J'ajoute b aux deux membres, puis je multiplie par a les deux membres de la
nouvelle équation obtenue »
En ajoutant b aux deux membres de cette équation, on obtient :
![]()
En multipliant les deux membres de cette dernière équation par a, on obtient :
![]()
Applications
1ère application
Trouve les nombres manquants dans les cases suivantes :
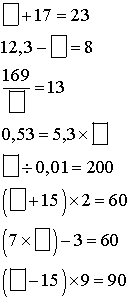
2ème application
Muhammad AL-KHAWARIZMI (780 env. - 850 env.) était un mathématicien arabe.
On te donne l’extrait de dialogue suivant : «
AL-KHAWARIZMI : Pense à un nombe
Raymond : C’est fait
AL-KHAWARIZMI : Ajoute lui 12
Raymond : C’est fait
AL-KHAWARIZMI : Multiplie le résultat par 3
Raymond : C’est fait
AL-KHAWARIZMI : Donne moi la réponse finale
Raymond : 51
AL-KHAWARIZMI : Le nombre auquel tu as pensé est 5 ».
Explique comment AL-KHAWARIZMI a-t-il procédé pour deviner le nombre pensé par Raymond.
3ème
application
Un
rectangle mesure 27 cm de longueur et 80 cm de périmètre.
Combien mesure la largeur ?
4ème
application
Peux-tu trouver dans combien d'années l'âge de ton père sera-t-il le double du tien ?
fractions et opérations sur les fractions
(groupes ciblés : cinquième, quatrième et
troisième)
De la cinquième à la troisième
A- Généralités
A1- Définitions
On donne deux nombres entiers naturels a et b, avec b différent de 0.

A2- Invariance
de la fraction et égalité de deux fractions
On ne change pas une fraction si on multiplie ou on divise son numérateur et son dénominateur par un même nombre différent de 0.

De
cette propriété se déduit donc l'égalité de
deux fractions.

Exemples
:
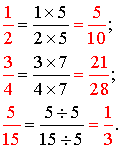
A3- Comparaison de fractions; ordre
De deux fractions de même dénominateur, la plus grande est celle qui possède le plus grand numérateur.
De deux fractions de même numérateur, la plus grande est celle qui possède le plus petit dénominateur.
Soit
a un nombre entier différent de 0 et quelconque.
On dira qu'un nombre entier b est un multiple de a si
et seulement s'il
![]()
Dans ce cas on dit également que a divise b ou
encore que a est un diviseur
de b.
Exemples :
8 est multiple de 4 car 8 = 2 × 4;
51 est multiple de 17 car 51 = 3 × 17.
0
est multiple de 9 car 0 = 0 × 9
Pour
comparer des fractions ayant des dénominateurs différents, il faut
d'abord les réduire au même dénominateur;
c'est-à-dire il faut trouver des fractions qui leur sont respectivement
égales et qui ont toutes le même dénominateur. Ce
dernier est un multiple commun à tous les
dénominateurs différents.
Exemples de comparaison de fractions :
![]()
Les dénominateurs différents sont 2, 4 et 8.
Un
multiple commun à ces dénominateurs est, par exemple, 8.
En effet 8 = 4 × 2 = 2 × 4.
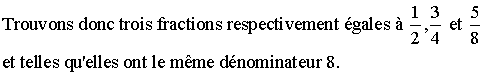
On ne change pas une fraction si on multiplie son numérateur et son dénominateur par un même nombre différent de 0.
Donc on a respectivement :
![]()
![]()
![]()
Les dénominateurs différents sont 3, 5 et 7. Un multiple commun de 3, 5 et 7
est 3 × 5 × 7 = 105.

On ne change pas une fraction si on multiplie son numérateur et son dénominateur par un même nombre différent de 0.
Donc on a respectivement :
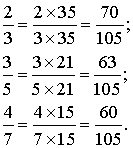
![]()
A4- Applications
1ère application
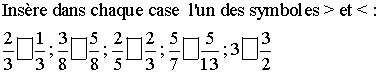
2ème application
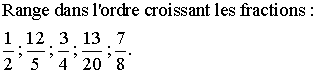
3ème application
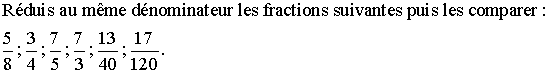
A5- Simplification d'une fraction
Simplifier une fraction consiste à trouver une fraction qui lui soit égale et dont le numérateur et le dénominateur sont deux nombres ayant 1et seulement 1 comme diviseur commun.
Pour
simplifier une fraction, il suffit de diviser son numérateur et son
dénominateur par un même nombre différent de 0. Généralement ce
nombre est un diviseur commun du numérateur et du dénominateur.
Ce procédé devra se poursuivre jusqu'à ce que le numérateur et le dénominateur
aient 1 et
seulement 1 comme diviseur commun.
Le
résultat de la simplification d'une fraction est souvent appelé fraction
irréductible.
Ainsi une fraction est dite irréductible si et
seulement si elle n'est plus simplifiable, c'est-à-dire son numérateur et
son dénominateur sont deux nombres ayant 1et
seulement 1 comme diviseur commun.
Simplifier une fraction ou la rendre irréductible veut dire la même chose.
Exemples de simplification de fractions :
![]()
35 = 5 × 7 et 125 = 5 × 5 × 5 ; donc 5 est un diviseur commun de 35 et 125.
On sait qu'on ne change pas une fraction si on divise son numérateur et son dénominateur par un même nombre différent de 0.
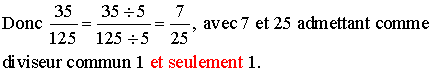
![]()
28 = 4 × 7 et 91 = 7 × 13 ; donc 7 est un diviseur commun de 28 et 91.
On sait qu'on ne change pas une fraction si on divise son numérateur et son dénominateur par un même nombre différent de 0.
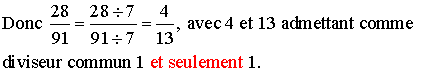
![]()
144
= 12 ×
12 = 3 ×
4 ×
3 ×
4 = 3 × 3 × 4 × 4 et
4320 = 432 × 10 = 3 × 144 × 2 × 5 = 3 × (3 × 3 × 4 × 4) × 2 × 5 =
2 × 3 × 3 × 3 × 4 × 4 × 5. Donc 3 ×
3 × 4 × 4 = 144 est un diviseur commun de
144 et 4320.
On sait qu'on ne change pas une fraction si on divise son numérateur et son dénominateur par un même nombre différent de 0.
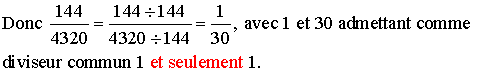
A6- Fraction d'une quantité
Soit Q une quantité quelconque.
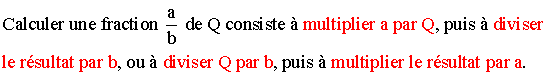
Application
:
Un
rectangle a pour longueur 15 cm et pour largeur 9 cm.
On réduit sa longueur d'un cinquième et sa largeur de tiers.
Calculer sa nouvelle surface et déduis de combien elle a été réduite.
A7- Écritures
fractionnaires d'un entier naturel et d'un nombre décimal
Tout
nombre entier naturel peut s'écrire sou la forme d'une fraction ayant 1 comme
dénominateur.
Exemples :
![]()
Tout nombre décimal peut s'écrire sous forme d'une fraction dont le dénominateur est une puissance de 10.
Exemples :
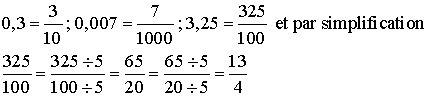
Quatrième et troisième
A- Opérations sur les fractions
A1- Addition
La somme de fractions de même dénominateur est égale à une fraction dont le numérateur est la somme de numérateurs et le dénominateur est le dénominateur commun.
Exemples :
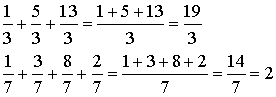
Somme de deux fractions de dénominateurs différents.
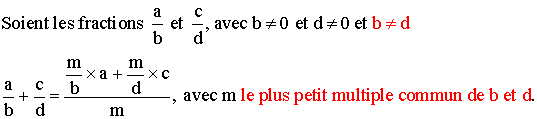
Généralisation de l'addition
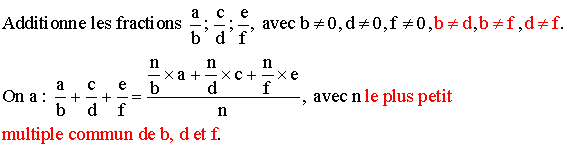
Exemple :
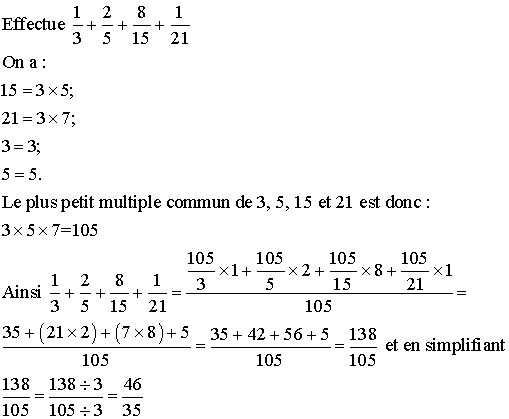
A2- Soustraction
Remarque importante : dans l'ensembles des fractions positives, la soustraction n'est possible que si le premier terme est supérieur ou égal au second terme.
Ainsi :
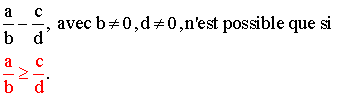
Quant à la méthode, elle est identique à celle évoquée pour l'addition.
Exemples
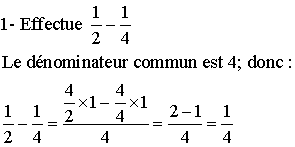
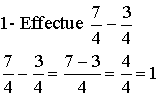
A3- Multiplication ou produit
La multiplication ou le produit de fractions est une fraction dont le numérateur est le produit des numérateurs et le dénominateur est le produit des dénominateurs.
Exemples
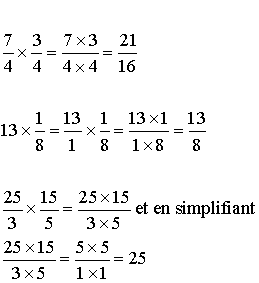
A4- Division

Exemples
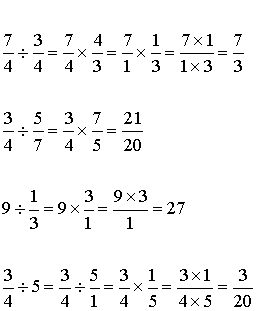
Troisième
A- Diviseurs et multiples communs à plusieurs nombres entiers
A1- Diviseurs communs
A11- Définitions
Soit
a un nombre entier quelconque.
On rappelle qu'un nombre b différent de 0 divise a si
et seulement s'il existe un nombre k tel que :
a = k × b
Dans ce cas on dira que b est un diviseur de
a ou a est divisible par b ou encore a est un multiple
de b.
Exemples :
3 divise 12 car 12 = 4 × 3;
7 divise 21 car 21 = 3 × 7;
13 divise 13 car 13 = 1 × 13;
3 divise 0 car 0 = 0 × 3;
1 divise 27 car 27 = 27 × 1;
1 divise 12 car 12 = 12 × 1;
A12- Propriétés
Tout nombre entier naturel différent de 0 divise 0; donc 0 admet une infinité de diviseurs tous différents de 0.
1 est diviseur de tout nombre entier naturel.
Tout nombre entier naturel différent de 0 admet au moins deux diviseurs : lui - même et 1.
A13- Recherche des diviseurs d'un nombre entier naturel
Considérons le nombre 12.
Ses diviseurs sont 1; 2; 3; 4; 6 et 12.
Ce sont là tous les diviseurs de 12.
L'ensemble des diviseurs de 12 est noté :
![]()
Si un nombre entier naturel a, différent de 0, n'admet que
lui-même et 1 comme diviseurs, c'est-à-dire :
![]()
alors a sera appelé nombre premier.
Exemple :
1; 2; 3; 5; 7; 11; 13; 17 sont tous des nombres premiers.
Comment donc a-t-on procédé pour trouver tous les diviseurs de 12 ?
Il faut d'abord trouver le plus petit nombre
premier différent de 1 et diviseur de 12; c'est donc 2.
On divise 12 par 2 et on obtient 6 comme quotient.
A son tour 6 admet également pour diviseur le plus petit nombre premier
différent de 1qui est 2.
On divise donc 6 par 2 et on obtient 3 comme quotient.
3 est premier; donc ses seuls diviseurs sont 1 et 3.
Finalement on a : 12 = 2 × 2 × 3 × 1 = 22 × 3 × 1
On a donc écrit 12 sous la forme d'un produit de puissances de nombres premiers.
C'est cette écriture qui nous a permis de
trouver tous les diviseurs de 12 : ce sont tous les
diviseurs de 22 × 3 × 1, c'est-à-dire 1;
2; 3;
22 × 1 = 4; 2
× 3 = 6; 22 × 3 = 12.
Prenons un autre exemple : cherchons tous les diviseurs de 144.
Le plus petit nombre premier différent de 1 et
divisant 144 est 2. Donc divisons 144 par 2; on
obtient 72 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 72 est 2.
Donc divisons 72 par 2; on obtient 36 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 36 est 2.
Donc divisons 36 par 2; on obtient 18 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 18 est 2.
Donc divisons 18 par 2; on obtient 9 comme quotient.
Le plus petit nombre premier différent de 1 et divisant 9 est 3.
Donc divisons 9 par 3; on obtient 3 comme quotient.
3 est premier; donc ses seuls diviseurs sont 1 et 3.
Finalement 144 = 24 × 32 ×
1 et les diviseurs de 144 sont :
1; 2; 3;
22 = 4; 2
× 3 = 6; 23 = 8; 32
= 9; 22
× 3 = 12; 24 =16;
2 × 32
= 18;
23 × 3 = 24; 22
× 32 = 36; 23
× 32 = 72; 24
× 32 × 1 = 144 et ainsi :
![]()
A14- Recherche des diviseurs communs de deux nombres entiers naturels différents de 0
Soient deux nombres entiers naturels a et b distincts et différents de 0.
un diviseur commun de a et b est un nombre différent
de 0 divisant à la fois a et b.
L'ensemble des diviseurs communs de a et b est donc :
![]()
Si
cet ensemble est égal à {1} alors on dira que a et b sont premiers
entre eux.
Ainsi 12 et 25 ont pour diviseur commun 1et seulement 1;
donc 12 et 25 sont premiers entre eux.
Exemple :
L'ensemble des diviseurs communs de 12 et 144 est :
![]()
Ainsi le plus grand diviseur commun (abréviation : p.g.d.c) de 144 et 12 est unique et est égal à 12.
A15- Simplification d'une fraction

A16- Applications
1ère Application : simplifions les fractions suivantes :
![]()

Écriture
de 680 :
Le plus petit des nombres premiers différent de 1et divisant 680 est 2;
donc divisons 680 par 2; on obtient pour quotient 340.
Le plus petit des nombres premiers différent de 1et divisant 340 est 2;
donc divisons 340 par 2; on obtient pour quotient 170.
Le plus petit des nombres premiers différent de 1et divisant 170 est 2;
donc divisons 170 par 2; on obtient pour quotient 85.
Le plus petit des nombres premiers différent de 1et divisant 85 est 5;
donc divisons 85 par 5; on obtient pour quotient 17.
17 est premier.
On a donc :
680 = 2 × 2 × 2 × 5 × 17 = 23 × 5 × 17
Écriture de 1240 :
Le plus petit des nombres premiers différent de 1et divisant 1240 est 2; donc divisons 1240 par 2; on obtient pour quotient 620.
Le
plus petit des nombres premiers différent de 1et divisant 620 est 2;
donc divisons 620 par 2; on obtient pour quotient 310.
Le
plus petit des nombres premiers différent de 1et divisant 310 est 2;
donc divisons 310 par 2; on obtient pour quotient 155.
Le
plus petit des nombres premiers différent de 1et divisant 155 est 5;
donc divisons 155 par 5; on obtient pour quotient 31.
31 est premier.
On a donc :
1240 = 2 × 2 × 2 × 5 × 31 = 23 × 5 × 31
Tout ce qui vient d'être dit se résume par les dispositions suivantes :
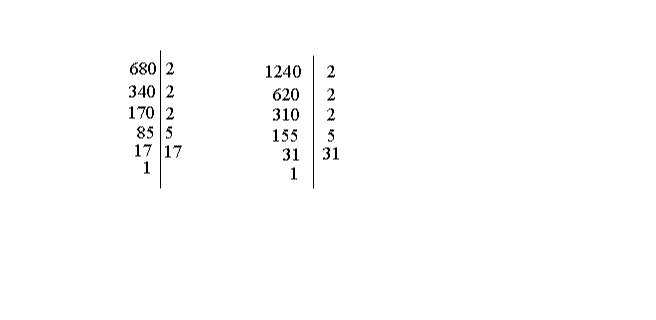
Le
p.g.c.d de 680 et 1240 s'obtient en prenant les facteurs premiers communs
et de plus faibles puissances et en effectuant leur
produit.
Ce sont 23 et 5. Leur produit est 23 × 5; donc le p.g.c.d
de 680 et 1240 est 23 × 5 = 8 × 5 = 40.
Pour
simplifier la fraction donnée, il suffit donc de diviser le numérateur et le
dénominateur par 40 et on obtient la fraction irréductible :
![]()
A toi de simplifier les trois autres fractions.
A2- Multiples communs
A21- Propriété
0 est multiple de tout nombre entier naturel différent de 0.
A22- Recherche des multiples d'un nombre entier naturel différent de 0
Soit a un nombre entier différent de 0.
L'ensemble des multiples de a est un ensemble infini et est défini par compréhension da la manière suivante :
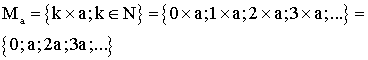
Exemple :
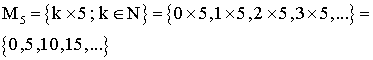
A23- Recherche des multiples communs de plusieurs nombres entiers naturels différents de 0
Soient plusieurs nombres entiers naturels a, b, c, d tous différents de 0.
L'ensembles des multiples communs de a, b, c et d est :
![]()
Exemple :
![]()
A24- Recherche du plus petit multiple commun de plusieurs nombres entiers naturels différents de 0
Soient plusieurs nombres entiers naturels a, b, c, d tous différents de 0.
L'ensembles des multiples communs de a, b, c et d est :
![]()
Cet ensemble possède un élément x0 tel que :
![]()
C'est le plus petit élément appartenant à l'intersection précitée. On le nomme plus petit multiple commun (abréviation : p.p.m.c) de a, b, c et d.
Pour trouver cet élément, on écrit d'abord les nombres a, b, c et d sous la forme de produits de puissances de facteurs premiers, puis on prend le produit de plus grandes puissances de ces facteurs, que ces derniers soient ou non communs.
Exemples :
Trouvons le p.p.m.c de 1240 et 680.
On a :

Donc
680 = 2 × 2 × 2 × 5 × 17 = 23 × 5 × 17
1240 = 2 × 2 × 2 × 5 × 31 = 23 × 5 × 31
p.p.m.c (680;1240) = 23 × 5 × 17 × 31 = 40 × 17 × 31 = 21080
Trouvons le p.p.m.c
de 1360 et 31000.
On doit d'abord trouver :
1360 = 24 × 5 × 17
31000 = 23 × 53 × 31
p.p.m.c
(1360;31000) = 24 × 53 × 17 × 31 = 16 × 125 × 17 ×
31 =
1054000
A25- Application de la notion de p.p.m.c
Dans une addition ou une soustraction de fractions, le dénominateur commun est le p.p.m.c des différents dénominateurs de ces fractions.
Exemple :

A26- Applications
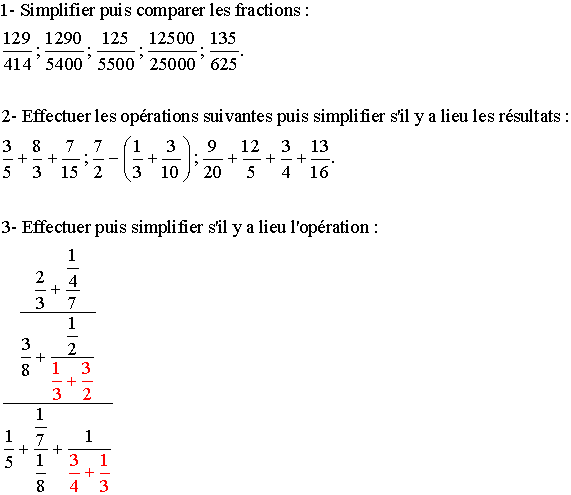
Indications
pour cet exercice :
Tu commences par les opérations élémentaires indiquées en rouge, puis
tu les remplaces par les résultats trouvés. Tu poursuis ensuite en procédant
de la même manière, jusqu'au dernier résultat et enfin tu simplifie s'il y a
lieu.