L'ATELIER DU COLLEGIEN (1)

Dessine sur ta feuille une droite quelconque que tu nommeras (d) . Prends sur (d) un point quelconque A . Prends également un point B n'appartenant pas à (d) .
Construis avec ta règle et ton compas le losange (ABCD) sachant que (d) est un de ses axes de symétrie . Quel est son second axe de symétrie ?

Dessine sur ta feuille deux droites quelconques non parallèles que tu nommeras d et d' .
Prends un point A ne leur appartenant pas .
Construis le cercle (C) passant par A tel que d et d' soient deux de ses axes de symétrie .
Combien un cercle possède-t-il d'axes de symétrie et quelle est leur propriété commune ?

retour au début de la page

droite graduée
(groupe ciblé : sixième)

Prends une droite graduée (tu pourras par exemple prendre pour unité de mesure des longueurs le centimètre) .
Sur cette droite place les points A, B, C et D sachant que :
l'abscisse de A est le double de celle de B;
l'abscisse de B est égale à celle de C diminuée de 3;
l'abscisse de C est la moitié de celle de D;
l'abscisse de D est 10 .

qui suis-je
(groupe ciblé : sixième)

Mes points ont tous l'abscisse égale à 0 . Je suis ............................ ;
Mes points ont tous l'ordonnée égale à 0 . Je suis ........................... ;
J'ai mon abscisse et mon ordonnée toutes deux égales à 0 . Je suis .......................... ;
Mes points ont chacun l'abscisse égale à l'ordonnée . Je suis .........................

retour au début de la page

parallélogramme
(groupe ciblé : cinquième)

Trouve deux énoncés tels que chacun te permette d'affirmer qu'un quadrilatère est un parallélogramme .

Quelle propriété doivent vérifier les côtés pour qu'un parallélogramme soit un rectangle ? un losange ?

Quelle propriété doivent vérifier ses diagonales pour qu'il soit un rectangle ? un losange ?

Quel est le quadrilatère qui est simultanément parallélogramme , rectangle et losange ? Quel angle fait chacune de ses diagonales avec l'un quelconque des côtés ?

(C) est un cercle muni de deux diamètres [AB] et [CD] non perpendiculaires .
Montre que le quadrilatère (ACBD) est un rectangle .

(MNP) est un triangle quelconque .
N' et P' sont respectivement les symétriques de N et de P par rapport à M .
Existe-il un parallélogramme dans la figure obtenue ? Justifie ta réponse .
Que doit vérifier l'angle au sommet M du triangle (MNP) pour que le quadrilatère précité soit un losange ?
Quelle doit être la nature de (MNP) pour que ce quadrilatère soit un rectangle ? un carré ?

retour au début de la page

symétrie axiale
(groupe ciblé : cinquième)

NB : la symétrie axiale est parfois nommée "symétrie orthogonale" .

Construis un triangle (ABC) isocèle de sommet A tel que |BC| = 2 cm et |AB| = 3 cm .
Construis K le symétrique de B par rapport à la droite (AC), et L, le symétrique de C par rapport à la droite (AB) .
Quelle est la nature du triangle (AKL) ?

symétrie centrale
(groupe ciblé : cinquième)

Construis un triangle (EFG) rectangle en E tel que |EF| = 3 cm et |EG| = 1 cm .
Construis F' le symétrique de F par rapport à E, et G', le symétrique de G par rapport à E .
Quelle est la nature du quadrilatère (FGF'G') ?

retour au début de la page

caractérisation d'un triangle isocèle
(groupe ciblé : cinquième)

Dans un triangle (ABC), on a les mesures des angles suivants :
mes([AB;[AC) = 78° ; mes([BA;[BC) = 24° .
Calcule la mesure de l'angle ([CA;[CB) et déduis - en la nature de ce triangle .

angles alternes - internes et angles correspondants
(groupe ciblé : cinquième)

Reproduis sur une page de ton cahier la figure suivante :

Qu'appelles - tu les angles suivantes :

A₁ et B₁ ; A₂ et B₂ ; A₃ et B₁ ; A₄ et B₂ ; A₂ et B₃ ; A₁ et B₂ ?

Compare leurs mesures lorsque les droites d et d' deviennent parallèles

Il faudra que tu te rappelles des méthodes suivantes :
dans un plan, pour démontrer que deux droites d et d' coupées par une sécante (xy) sont parallèles il suffit de démontrer l'une des propriétés suivantes :
- d et d' forment avec (xy) des angles alternes-internes de mesures égales;
- d et d' forment avec (xy) des angles alternes-externes de mesures égales;
- d et d' forment avec (xy) des angles correspondants de mesures égales;
- d et d' forment avec (xy) des angles intérieurs supplémentaires.

retour au début de la page

animations
(groupe ciblé : cinquième)

Tu vas te servir de ta règle et de ton compas pour procéder aux constructions géométriques qui suivent :

1- On te donne un segment [AB] quelconque et on te demande de construire sa médiatrice;

2- On te donne une droite (d) quelconque et un point A quelconque n'appartenant pas à (d). On te demande de construire la droite parallèle à (d) et passant par A;

3- On te donne un angle ([Ox , [Oy) de sommet O et on te demande de construire sa bissectrice.

Pour t'aider, ouvre les pages suivantes :

animation 6 relative à la première question;

animation 7 relative à la seconde question;

animation 8 relative à la troisième question.

calcul numérique
(groupe ciblé : quatrième)

On te donne a = 0,5 ; b = -2 et c = (b)³ .
Calcule les expressions suivantes :
A = a×b³ ; B = (a×b)³ ; C = a -b×c ; D = (a-b)×c ; E = a³ × b³ ; F = a×c-b×c .
Que peux-tu affirmer pour B et E ?
Écris la formule générale qui correspond à ton affirmation .
Que peux-tu affirmer pour D et F ?
Écris la formule générale qui correspond à ton affirmation .

retour au début de la page

fraction complexe
(groupe ciblé : quatrième)

Calcule l'expression suivante :

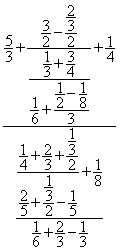
Tu commenceras par effectuer les opérations élémentaires , puis tu les remplaceras par les résultats élémentaires , ceci jusqu'à réduire cette fraction complexe à sa plus simple expression .

retour au début de la page

mathématique de la fourmi
(groupes ciblés : quatrième et troisième)

Qu'est-ce que le cosinus d'un angle ?

Dessine sur ta feuille un triangle rectangle (ABC) rectangle en A . Les angles aigus sont
([BA ; [BC) et ([CA ; [CB) . Pour simplifier les écritures posons B = mes.([BA ; [BC) et C = mes.([CA ; [CB) en degrés .

Par définition, les rapports suivants :

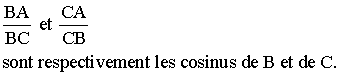
Les arabes déclaraient que dans un triangle rectangle, le cosinus d'un quelconque de ses aigus est le rapport du côté qui lui est adjacent à l'hypoténuse .
Cette affirmation reste vraie à nos jours . Nous remarquons, par exemple, que le côté autre que l'hypoténuse, adjacent à ([BA ; [BC) est [BA] .

Les égyptiens, utilisaient le cosinus dans leurs travaux relatifs à l'agriculture sur leurs terrains longeant le Nil. Quant aux grecs, ils l'utilisaient dans leurs travaux de constructions et d'architecture .

Extension de la notion de cosinus à un angle quelconque, aigu ou obtus; saillant ou entrant.

Prends sur ta feuille un axe gradué (x'Ox) d'origine O . L'unité de mesure sur cet axe sera par exemple le centimètre .
Place les nombres relatifs -2 ; -1 ; 0 ; +1 ; +2 .
Trace le cercle de centre O et de rayon r = 1cm . Il coupera l'axe (x'Ox) en deux points P et Q d'abscisses respectives -1 et +1 .

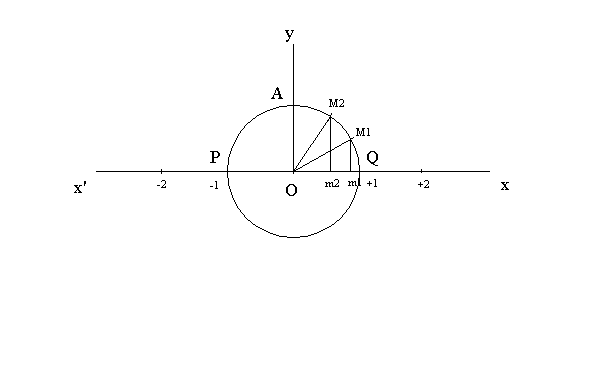
Imaginons une fourmi M se déplaçant sur le cercle en prenant départ du point Q . Tu vas supposer qu'elle s'y déplace dans le sens (QAP) ; A étant l'intersection de la perpendiculaire(Oy) à l'axe gradué élevée de O .

A chacune de ses positions, la fourmi forme avec O et l'axe gradué un angle ([OQ ; [OM) .
Par définition, le cosinus de cet angle est l'abscisse de la projection orthogonale m de M sur l'axe gradué .
Posons pour simplifier, mes ([OQ ; [OM) = a .

Ainsi, à la position M1 tu obtiens :

A la position M2 tu obtiens :

(groupe ciblé : quatrième)

Pour ce groupe la fourmi n'aura pas à franchir le point A ; ainsi l'étude du cosinus d'un angle se limitera aux valeurs de la mesure de l'angle ([OQ ; [OM) comprises entre 0° et 90°.

Donne les valeurs suivantes (sans utilisation de ta calculatrice) en utilisant la figure ci-dessus :
cos 0° ; cos 45° ; cos 60° ; cos 30° ; cos 90° .

Place exactement le point m₃ tel que :

Place exactement le point m₄ tel que :

(groupe ciblé : troisième)

Pour ce groupe, la fourmi se déplacera du point Q au point P; elle ne pourra pas franchir ce dernier . Ainsi la mesure de ([OQ ; [OM) variera de 0° à 180° .

Donne les valeurs suivantes (sans utilisation de ta calculatrice) en utilisant la figure ci-dessus :
cos 120° ; cos 135° ; cos 150° et cos 180° .

prends maintenant une valeur quelconque de a .
Compare en t'aidant de la figure le cosinus de a et celui de (180° - a) .
Qu'en déduis-tu ? Complète l'énoncé suivant : " deux angles ................ ont leurs cosinus opposés . "

Sur la figure ci-dessus reproduite sur une page de ton cahier, tu vas maintenant travailler sur l'axe gradué (y'Oy) perpendiculaire à (x'Ox) en O et ayant même unité que (x'Ox) .

Tu obtiens ainsi un système de repère orthonormé (O ; x'x ; y'y) .

A chacune des positions M de la fourmi, considère m' la projection orthogonale de M sur l'axe (y'Oy) .
Par définition, le sinus de l'angle ([OQ ; [OM) est l'ordonnée de la projection orthogonale m' de M, ou encore l'ordonnée de M .

Ceci dit, donne les valeurs suivantes (sans utilisation de ta calculatrice) en utilisant la figure :
sin 0° ; sin 30° ; sin 60° ; sin 45° ; sin 90° ; sin 120° ; sin 135° ; sin 150° ; sin 180° .

a = mes ([OQ ; [OM) étant maintenant quelconque et en t'aidant de la figure, complète
les deux énoncés suivantes :

" deux angles ..................ont leurs sinus égaux "
" deux angles complémentaires sont tels que ...................."

La fourmi se déplaçant entre Q et A, complète les relations suivantes :

sin a ..... cos (a + 90°) et cos a ..... sin (a + 90°) .

retour au début de la page

constructions géométriques
(groupe ciblé : quatrième)

1- Construis un triangle (MNP) tel que MN = 8 cm et tel que le cercle qui lui est inscrit ait pour rayon 2 cm .

2- Construis un triangle (QRS) tel QR = 8 cm et tel que la distance entre le centre du cercle qui lui est inscrit et la droite (RS) soit égale à 2,5 cm .

3- Construis un trapèze (LMNP) dont les bases sont [LM] et [NP] et tel que LM = LP = 4 cm et NP = 7 cm .
Les droites (LP) et (MN) se coupent en O . On pose OL = y .
Démontre que :

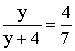
Calcule OL .

propriété des bissectrices intérieure et extérieure
de l'angle d'un triangle
(groupe ciblé : quatrième)

On te donne un triangle quelconque (ABC) .
Construis avec ton compas la bissectrice intérieure [Ax et la bissectrice extérieure [Ay de l'angle ([AB ; [AC) .
[Ax et [Ay coupent (BC) respectivement en M et N .
Démontre que l'on a :

On suppose que (BC) est gradué et orienté (sens positif : B vers C) . Démontre que :

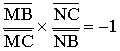
On dira alors que les points M et N partagent le segment [BC] dans une division harmonique que l'on note (B , C , M , N) = -1 .
Complète l'énoncé : " Dans un triangle, les bissectrices intérieure et .......... d'un angle au sommet quelconque partagent le .......... opposé dans une division harmonique " .

Dessine sur ta page deux angles adjacents et supplémentaires ([Sx ; [Sy) et ([Sy ; [Sz) .
Soient [St et [St' leurs bissectrices respectives .
Que peux-tu affirmer pour l'angle que forment ces bissectrices ?
Soit une droite quelconque (d) qui rencontre [Sx ; [Sy ; [St et [St' respectivement en M ; N ; M' et N' .
Démontre que (M , N , M' , N') est une division harmonique . On dira que le faisceau de demi-droites ([Sx ; [Sy ; [St ; [St') est un faisceau harmonique .

Reviens au triangle (ABC) du début de ton exercice .
Démontre que :

retour au début de la page

lieu géométrique
(groupes ciblés : quatrième et troisième)

Dans un plan on te donne deux points fixes A et B tels que AB = 7 cm .
Trouve l'ensemble des points M de ce plan tels que :

Pour t'aider dans la recherche du lieu géométrique de M, ouvre la page animation 1.

produit de symétries
(groupe ciblé : troisième)

Sur ta feuille prends deux symétries centrales S_o et S_o' respectivement de centres O et O' .

Soit f un objet mathématique quelconque . Soit f₁ son image par S_o et f₂ l'image de f₁
par S_o' . Par définition l'image de f par la transformation " S_o suivie de S_o' " est f₂ .
S_o suivie de S_o' sera notée : S_o' o S_o et tu écriras donc :
(S_o' o S_o )(f) = (S_o' )((S_o )(f)) = (S_o' )(f₁ ) = f₂ .

Soit maintenant un point M quelconque sur ta feuille de dessin différent de O et de O' .
Soit m l'image de M par S_o . Tu écriras donc S_o (M) = m .
Place m .
Soit m' l'image de m par S_o' . tu écriras S_o' (m) = m' .
Place m' .
Tu pourras également écrire : (S_o' o S_o )(M) = (S_o' )((S_o )(M)) =
(S_o' )(m) = m' .
Démontre l'égalité :

Dans un repère orthonormé , O a pour abscisse 1 et pour
ordonnée 2 ; O' a pour abscisse 2 et pour ordonnée 3 .
Sachant que M a pour abscisse - 1 et pour ordonnée - 2 , calcule
les coordonnées du point m' .

retour au début de la page

encore Thalès
(groupe ciblé : troisième)

On te donne un triangle quelconque (ABC).

Trouve un procédé géométrique (avec la règle et le compas) te permettant de partager ce triangle en trois triangles d'aires égales.

Trace, par exemple, la hauteur [AH], H appartenant à [BC].

Si h et a sont respectivement les mesures géométriques de [AH] et [BC], alors l'aire S du triangle (ABC) est :

Les trois triangles issus de ce partage auront un sommet commun A, une hauteur commune [AH] et une aire commune qui est égale à :

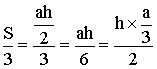
Cette dernière expression montre qu’il suffit de partager géométriquement le segment [BC] en trois parties égales.

La méthode géométrique de partage d'un segment en n parties de mesures égales est illustrée par l'animation 10.

résolution des équations du second degré ramenées à des produits de facteurs du premier degré
(groupe ciblé : troisième)

Résous dans R les équations suivantes :

(3x - 2)(4x + 5) + 5(2 - 3x) = 0 ;

9x² - 64 = 0 ;

x² - 16 = -x + 4 ;

(3x + 4)² = 9 ;

(2x - 1)(3x + 1) + 4x(1 - 2x) (-3x - 1) = - 4x² (2x - 1)(3x + 1) .

Tu utiliseras pour cela des identités remarquables afin de transformer les expressions définissant ces équations en produits de facteurs du premier degré , puis tu résoudras l'équation transformée de la forme :
A × B = 0 ou A × B × C = 0 .

retour au début de la page

applications affines et un peu de géométrie analytique
(groupe ciblé : troisième)

1) On te donne l'équation suivante :
(m - 1)x + n = 0 , avec m et n deux paramètres réels .
Étudie l'existence de la racine suivant les valeurs de m et n .

2) Tu supposes par la suite m différent de 1 et n égal à 1 .
Soit l'application affine f_m (x) = (m - 1)x + 1 .

Montre que toutes les courbes D_m passent par un point fixe A
dont tu calculeras les coordonnées .
Détermine l'équation de la droite D'_m passant par A et
perpendiculaire à D_m .
Soit B l'intersection de D'_m et de l'axe x'Ox des abscisses .
Détermine les coordonnées de B , ainsi que l'équation de la droite
D"_m passant par B et parallèle à D_m .

3) Soit B' l'intersection de D_m et de l'axe des abscisses .
Connaissant les coordonnées respectives de A , B , B' vérifie
que tu as les relations suivantes dans le triangle (ABB') rectangle
en A :

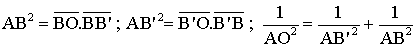
Ce sont là les relations métriques vérifiées par tout triangle rectangle .
Les deux premières s'énoncent :" chaque côté de l'angle droit
est la moyenne proportionnelle de sa projection orthogonale
sur l'hypoténuse et l'hypoténuse entière " .

La dernière s'énonce :" l'inverse du carré de la hauteur relative
à l'hypoténuse est égale à la somme des inverses des carrés
des deux côtés de l'angle droit " .

retour au début de la page

vecteurs et translations
(groupe ciblé : troisième)

A (0 ; 1) ; B (-4 ; 2) et C (5 ; 4) .

Détermine les coordonnées du centre de gravité G de ce triangle .
Détermine les coordonnées des sommets du triangle (A'B'C') ,
image ou transformé de (ABC) par t , ainsi que les coordonnées de
son centre de gravité G' .

Détermine les coordonnées de l'orthocentre F et du triangle (A'B'C') .

Soit M le centre du cercle (L) circonscrit au triangle (ABC) .
Calcule le rayon de (L) .

Si M' est le centre du cercle (L') circonscrit au triangle (A'B'C') ,
utilise la translation t pour déterminer les coordonnées de M' et
calcule le rayon de (L') .

Complète l'énoncé :" la translation conserve le ............du cercle " .

Calcule les aires S et S' des deux triangles (ABC) et (A'B'C') .

Complète l'énoncé :" la translation conserve .............du triangle " .

retour au début de la page

page 2 page 3